Péter TÓTH, Kinga HORVÁTH
The development level of pedagogical students’ inductive thinking in the 21st century
Introduction
Owing to the requirements of a knowledge-based economy, the role of higher education has been appreciated during the latest decades. Therefore, third and fourth-generation universities have become committed to developing those competencies of their students that make them able to meet the dynamically changing requirements of modern societies and work positions (Kozma & Pusztai, 2018; Gordon, 2003; Lukovics & Zuti, 2014). Moreover, competence development has been at the core of higher grade training besides teaching vocational knowledge.
According to several types of research, the labor market is expressing a solid demand so that career-starters should, in addition to their vocational knowledge, possess developed communication, organization, and problem-solving skills as well as analog and logical thinking, creativity, interpersonal skills, emotional intelligence and should be assertive and apt to be motivated. Professional literature calls these labor market key competencies (soft skills). However, the researchers also point to the fact that it is precisely these competencies in terms which career starter employees are unprepared when arriving from higher education to the labor market (Engler, 2019); companies often consider these competencies more critical than vocational preparedness (Veroszta & Nyüsti, 2015) and call the trainers to develop these skills (Kautz et al., 2014). According to a study by the Manpower Group (2015), 16 percent of the positions have remained unfilled owing to the lack of soft skills in Europe. The opinions about what competencies belong to soft skills are very diverse. Career-starters show the most deficiencies in intra- and interpersonal and some cognitive competencies and attitudes. Several studies refer to serious shortages in the so-called higher-level reasoning, including problem-solving, critical thinking, judging, and decision-making ability. At the same time, in the world of labor, these appear as demands in their organic relation system (Balcar, 2014; Carnevale, 2013; Eger & Grossmann, 2004; Cornalli, 2018).
In higher education, pedagogical and teacher training plays a unique and outstanding role in many respects. The training does not only aim to develop the students' specific labor market competencies but to make them ready and able to develop the labor market competencies of their students, as well. So in training programs, the competence requirements teacher students meet must also include the methodology of developing these competencies.
Higher education can fulfill this requirement in case educators working in teacher training (1) are aware of what the key competencies of the pedagogic profession are, (2) know the development level of the competencies of the future pedagogic professionals, (3) are aware of the competing demands of the schools, and (4) know how the competencies presented in point (1) can be diversely developed so that by the end of the training the difference between the expected and the current competence levels can be as trim as possible.
According to another point of view, these soft skills are vital competencies, and their attainment influences the quality of teaching in public education. Furthermore, this is a decisive factor in promoting effective learning (Tang, 2013). At the same time, teaching is also a complex activity that needs a comprehensive set of knowledge and skills, including hard and soft skills, so that the teacher can handle classroom needs and problems successfully (Tang et al., 2015b; Flores & Day, 2006).
Consequently, teacher trainers face the challenge of how future teachers can be prepared to meet the labor market requirements; the school, in this case, takes the students' age characteristics and personal endowments into consideration.
It cannot be postponed any longer – developing soft skills must be given more significant stress in teacher training and in-service training programs, primarily in the methodologies.
In order to be able to meet the presented requirements, the trainers must be able to assess the development level of pedagogical students' competencies. Hence, not being reliable and valid measuring tools for each soft skill. Logical reasoning and its components, rule induction, and analog and diagrammatic reasoning do not belong to this group.
Thus, this research can be considered a kind of a "situation analysis" as it was aimed to get to know what development level the education students entering higher education are at in terms of logical thinking, which is one of the labor market's key competencies (soft skills), i.e., what is the initial competence level in this field.
Conceptual background
Concept of Soft Skills
As presented above, in addition to professional successes, or instead as their preconditions, the so-called soft skills are getting increasingly important and play a significant role in employability and achieving wealth and personal objectives.
Some authors identify soft skills with other characteristics; for example, Verma (2013) draws a parallel between soft skills and emotional intelligence, saying that a person more developed than the average can positively manage other people's behavior and positively impact them. Others think that soft skills are synonyms for employability (Prasad & Nagendra 2017), which indicates that to improve the chances of getting employed, one must have, in addition to his/her technical competencies, these skills and competencies throughout his/her life. Carneiro et al. (2007) stress the social utilization of soft skills. Besides this, by putting the aspects of using info-communication tools into the foreground, Meacham et al. (2014) distinguish between old and new soft skills. Communication skills, the ability to react, and teamwork appear in the new category, as well but already in the context of application in the online space.
It has been proved that the critical competencies demanded by employers are of fundamental importance in successfully implementing work activities (Pachauri & Yadav, 2012; Orlando & Altomari, 2019). These include employee engagement, interpersonal competencies, practical communication skills, emotional self-control, and problem-solving (Carnochan et al., 2014). These inter-and intrapersonal competencies refer to personality, attitudes, and behavior (Moss & Tilly, 2001) as well as aims, motifs, and personal preferences (Heckman & Kautz, 2012). This personality-specific competency determines one's strengths as a leader, facilitator, or mediator (Robles, 2012; Pisoňová, 2017). Cognitive and metacognitive skills represent the dynamic combination of intellectual and practical competencies (Haselberger et al., 2012, Cinque, 2016) that keep developing throughout one's life (Knight & Page, 2007) and are inevitable in community existence and workplace successes (Kechagias, 2011).
Teachers' Soft Skills
Soft skills can be developed the most effective during education, so teachers play a decisive role in this process.
It is important to emphasize that the teachers do not only have to adapt to the requirements of the pupils and their parents (Brewster & Railsback, 2001) and must provide the effectiveness of the teaching-learning process (Pellerey, 2017) but also have to meet social and labor market expectancies (Bauman, 2011). Therefore, the development of transversal competencies (Svecnik, 2008; Tang et al. 2015a; Orlando & Altomari, 2019), known as teacher competencies, is a prime target. The comparative research that was implemented in 2011 and 2018 with the involvement of first-grade teacher students and that examined the attitudes toward teacher competencies, abilities, and skills as well as to other knowledge and forms of behavior found that some capabilities (professional behavior, the ability to perform high-quality work, the ability to defend and protect, health consciousness, environmental consciousness, and moral competence) were judged significantly more critical by correspondence students than by full-time students.
According to Hattie (2003), teachers with developed soft skills exert direct influence on their pupils' interest, engagement, and the evolution of their future capacities (Salleh et al., 2010), and their role is vital in improving self-evaluation, self-knowledge, and other personal characteristics (Tang et al. 2015a; Csehiová & Kanczné, 2019; Csehiová, Kanczné Nagy & Tóth-Bakos, 2020; Baka, L. P., 2021).
Soft skills play an outstandingly important role in interpreting and understanding complex situations; therefore, they must be paid attention to when compiling the teacher training program. Many studies dealing with the soft skills needed for effective and successful teaching (Tang, 2018; Rashidi et al., 2018; Orlando & Altomari, 2019) distinguish between five components: communication, leadership and direction, teamwork, life-long learning, and problem-solving. Other authors mention specific moral characteristics, professional knowledge, and entrepreneurial competence (Pachauri & Yadav, 2012; Tang, et al., 2015b). Tang et al. (2015c) found that the five soft skills (teamwork, communication, leadership skills, critical thinking, and problem-solving) are significantly connected to the restfulness of teaching.
Using developed problem-solving skills, teachers' thinking may become critical, creative, innovative, and analyzing, which is of outstanding importance since, by way of these, they can offer their students new ideas and alternative solution possibilities (Orlando & Altomari, 2019). In cognitive pedagogy and psychology, the development of cognitive competencies has long been one of the essential education objectives (Resnick, 1987), as they include the ability to reason and explain, abstract notions, apply rules and draw conclusions (Holmes, 2002) as well as to gain and utilize new knowledge or use existing knowledge during the solution of new problems (Molnár et al. 2013).
Thinking is the base for all cognitive activities or processes characterizing humankind (Wu, 2011) and is the highest level of acquiring knowledge. The changes in individual thinking that appear in various contexts originate from the actual mutual effect of the cognitive system and the available environmental structure (Plumert, 2008). The personal ability to think in a disciplined way or to build one's thoughts on facts and proofs is known as the skill of logical Thinking (Wu, 2011). The ability to think logically means that logic is built into the thinking process when a problem is analyzed to find a solution. Logical thinking means that one sets reasonable goals, implements adequate operations according to the goals and hypotheses, and, considering the available proofs, comes to conclusions that prove or confuse one's hypotheses (Stanovich et al., 2008). The capability of analytic and logical thinking makes it possible to comprehend complex interrelations, transplant the gained information into a new structure quickly, and interpret it to solve the new problem.
Role of Inductive Reasoning in Problem Solving
Carroll (1993) mentioned inductive and deductive cognition as the "sub-skills" of the capacity of logical cognition. Inductive thinking is needed primarily when observations and experiences can be used in totally new (problem-solving of productive nature) or partly new, similar situations (problem-solving of reproductive nature). The new knowledge gained during such a process always bears the possibility of uncertainty and mistake. The main aim of inductive reasoning is to recognize regularities and generalizations (Mousa, 2017). According to Klauer (1999), the process of comparing is one of the essential characteristics of inductive reasoning. During this process, it is defined in the first step as the characteristics of the elements of reality and the relations between the specific elements, then similarities and differences are observed using which rules are recognized. Finally, generalizations and predictions can be formulated based on the rules identified while analyzing the observed cases; in this phase, inductive conclusions can be drawn.
Inductive thinking or reasoning plays an outstanding role in the cognition processes; it is understood as a general cognition capability (Pellegrino & Glaser, 1984; Molnár et al., 2013) that is connected to almost each higher-level cognition skill (Csapó, 1997; Molnár et al., 2013; Schubert et al., 2012; Alrawili et al., 2020), like for example, general intelligence (Klauer & Phye, 2008), the skills of gaining and applying knowledge (Hamers et al., 2000), abstract thinking (Goswami, 1991) or problem-solving.
Inductive reasoning is also referred to as the means of gaining new knowledge and the indicator of the learning potential and is also assigned an essential role in the transferability of knowledge (Resing, 1993). Research aimed at the exploration of general intelligence keeps count of it as one of the decisive factors in the effectiveness of the various operational processes of cognition (Carroll, 1993; Demetriou et al., 2011). The empiric research conducted with students starting their university studies and focused on inductive reasoning made it clear (Pásztor, 2019) that a quarter of the students were likely to face learning difficulties during their university years.
Research Aim and Research Questions
As presented above, inductive thinking is vital in teacher training as a soft skill. It is an essential key competence of the training, which must be developed – for two reasons. First, it plays an essential role in gaining knowledge, and so successful learning, for each teacher-student, and on the other hand, if highly developed, it will allow future teachers to improve their pupils' inductive thinking effectively.
In order that teacher training can fulfill its tasks effectively, educators must know and be able to examine the teacher candidates' key competencies, particularly their inductive thinking. This double aim makes this research especially timely.
Taking all this into consideration, the aim of this research was to
· describe the development level of first-grade teacher students' inductive reasoning,
· analyze the time spent on solving the tasks and task items,
· explore the relationship between the time consumed and the performance achieved in the inductive test.
Methodology of Research
General Background
From the time used for task solution, the speed of thinking can be concluded, allowing the determination of specific performance.
Specific performance indicates restfulness and can be described as the fraction of the consumed time and the achieved score.
According to Carroll (1993), those possessing more developed thinking skills can solve mathematical problems faster than people with weaker capacities, so there is a correlation between the development level and the pace of cognition (cited by: Sternberg & Ben-Zeev, 1996). Some query this standpoint (Winch, 1990). According to Sternberg and Pellegrino (cited by: Sternberg, 1985), the time used to choose a correct answer can predict the performance more precisely than the skill level itself.
Other researches were aimed at whether it was possible to conclude the item's difficulty level from the solution time. For example, Jacobs and Vandeventer (1968) said that the difficulty level of the items did have a correlation with the number of characteristics to be compared or remembered simultaneously; i.e., those achieving better results were able to keep several issues in mind at one time, but this could also mean that they dedicated more time to solve the given item (Georgiev, 2008). On the other hand, Vodegel Matzen et al. (1994) refer to Home and Habon's work which found that no conclusion can be drawn concerning the difficulty level of the items based on time consumption.
In this research, the tests developed by Psychometric Success WikiJob Ltd. (UK, London) were applied, paying particular attention to labor market demands (Newton & Bristol, n.s.). When developing the test, the experts based their measurement tools on one- and multifactor intelligence tests (Sternberg, 1985). The sample tasks of the test are available here: https://psychometric-success.com/.
According to Spearman (1927), the persons achieving good results in specific skill tests achieve good results in other performance tests, like mathematical tests or a worksheet measuring spatial skills; similarly, those producing weaker results in the given skill test will perform more weakly. Therefore, he thought one or more common factors concerning solving all intellectual tasks were the clues to success (Mackintosh, 1998).
Spearman (1927) divided the g-factor into two parts: (1) implicative logical (eductive) skills and (2) reproductive skills connecting to the storage and recall of information. For example, the Raven or the test applied in this research (Newton, Bristol, n.s.) belongs to the former.
Eductive competencies refer to logical operations based on a conclusion through which new knowledge is created from the perceived information through recognizing and comprehending interconnections and considering the contextual content.
A holistic approach is needed to understand the whole of the problem, while its solution demands the ability to recognize the relations and interdependences between the parts. Understanding the problem is more than comprehensive pattern recognition (Gestalt); highlighting the essence and neglecting unimportant elements is also necessary. In most cases, these cannot be verbalized; therefore, the measuring tools mainly consist of geometrical figures (squares, polygons, circles, etc.). The perception of these geometrical forms, the recognition of their typical characteristics, and the comprehension of the relations between them are dependent on the existing knowledge on the one hand and specific cultural effects on the other (Kane & Brand, 2003). The previous one is in harmony with the inductive operations (Klauer & Phye, 2008). As for the latter, one of the main advantages of the test must be stressed: it is, to a certain extent, culture-independent.
Instrument
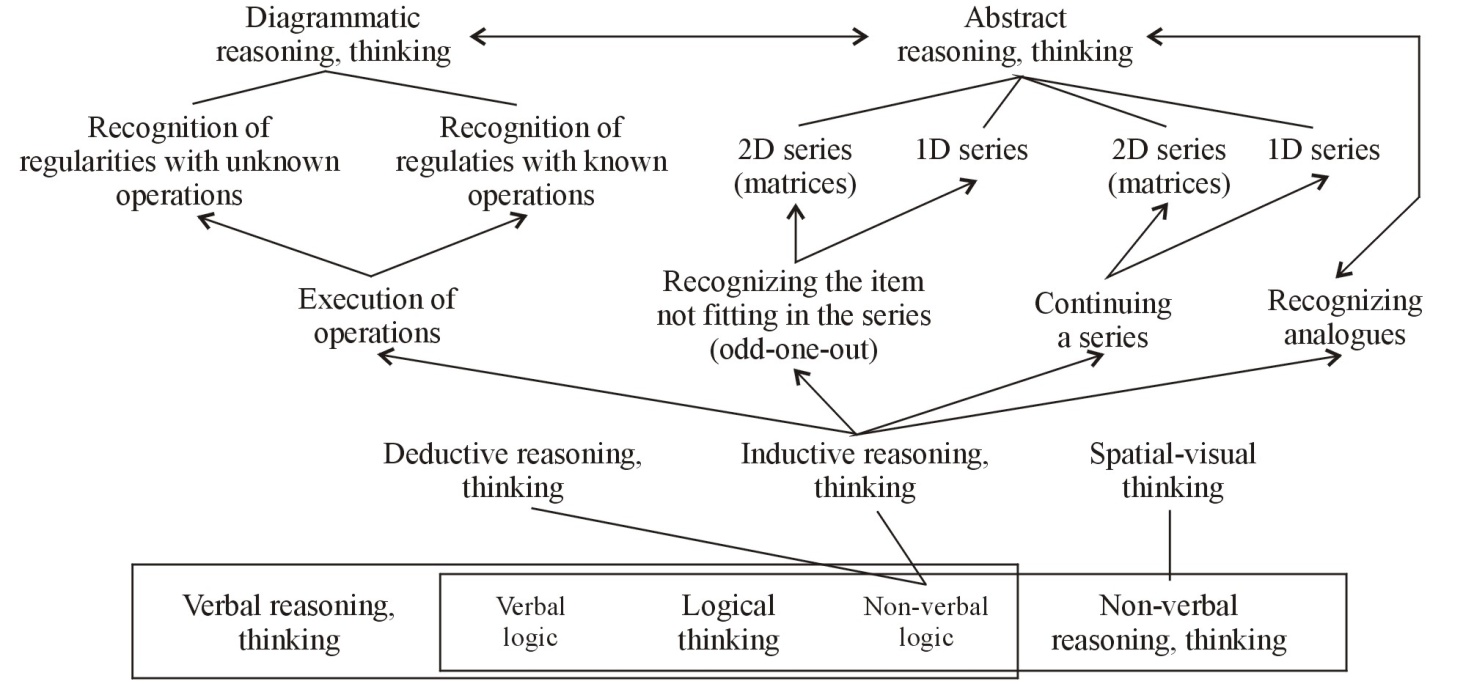
To examine cognition based on inductive implications, Newton and Bristol (n.a.) elaborated on the skill structure presented in Figure 1.
Figure 1.: The task system examining inductive cognition

In this research, an inductive reasoning test made of 30 items was applied, which consisted of the following task types:
· Task1: Continuation of one-dimension series (6 items);
· Task2: Recognition of the (' odd-one-out) elements not fitting in the one-dimension series (6 items);
· Task3: Recognizing an analog (6 items);
· Task4: Recognizing regularity – unknown operation (diagrammatic cognition) (6 items);
· Task5: Recognizing regularity – known operation (diagrammatic cognition) (6 items).
Online tests were applied during the research, which allowed to measure the time used for specific items. This was necessary for research objectives 2 and 3.
Data Analysis
First, the outcomes of the online measurement were examined by descriptive statistical analysis. The characteristics and structure of the components of inductive reasoning were determined by the univariate analysis. The mean and the standard deviation of the certain variables and the quartile values were also given first by tasks, then according to the components of inductive reasoning (abstract, diagrammatic and analog reasoning) for the whole sample, and finally, in terms of the certain background variables (type of training, specialization, gender, place of stay during the studies), too. The variables' values also define the confidence interval by 95% probability. Since most of the variables were not of normal distribution, the Mann-Whitney test was applied to compare certain sub-samples to see whether they were significant differences.
Tasks also made a statistical analysis of time consumption in order to be able to observe the inner correlations of their difficulties. Online measurement also allowed for analysis of the sound and wrong answers.
To examine the relationship between time consumption and inductive reasoning, the concept of specific performance was introduced, using which the performance of the students with the best results was compared. In the inductive test, specific performance was understood as the time necessary to achieve a unit of the score, which was defined as the ratio of consumed time and the score achieved by items: Timex/scores, where Timex indicated the time spent on solving task x (6 items) by seconds, while scores represented the score reached during this time.
Regression analysis was used to define the relationship between the score achieved in the test and time consumption and to determine how many percent of the variance the model accounted for.
Based on time consumption and the achieved scores, homogenous groups were created by cluster analysis of the whole sample, and then, by using the background variables, we specified their characteristics. Finally, reliability was checked by the K-means test.
Participants
The research, implemented in 2019 at the Faculty of Education at J. Selye University, Komarno, Slovakia, involved 204 first-grade teacher students. The demographical data of the participants are summarized below:
· Sex: 17.6% (N=36) male, 82.4% (N=168) female;
· Age: M=25.10 years, Modus: 20 years, SD=8.267 years, 76 persons (37.2%) between 19 and 20, while 49 persons (24.0%) between 21 and 22;
· Father's highest education level: primary school 9 persons (4.4%), trade school with no graduation exam 85 persons (41.7%), vocational secondary school 72 persons (35.3%), grammar school 18 persons (8.8%), higher education 20 persons (9.8%);
· Mother's highest education level: primary school 17 persons (8.3%), trade school with no graduation exam 47 persons (23.0%), vocational secondary school 85 persons (41.7%), grammar school 24 persons (11.8%), higher education 31 persons (18.2%);
· Place of living: city 92 persons (45.1%), other settlement 112 (54.9%); Country of secondary school graduation exam: Slovakia 120 persons (58.8%), Hungary 83 persons (40.7%);
· Type of the school of secondary school graduation: four-grade grammar school 70 persons (34.3%), eight-grade grammar school 9 persons (4.4%), vocational secondary school 113 persons (55.4%) and adult education 12 persons (5.9%). Rate of those having taken their secondary school graduation exams at Hungarian speaking vocational secondary schools in Slovakia: 60%, while this number is only 48.8% with those having taken their graduation exams in Hungary;
· Language of teaching at secondary school: Hungarian 182 persons (89.2%), Slovakian 12 persons (5.9%), bilingual 10 persons (4.9%);
· Specialization: teacher training 57 persons (27.9%), pre-school teacher education 127 persons (62.3%), pedagogy and public education 19 persons (9.3%);
· Training: full-time 145 persons (71.1%), correspondence 59 persons (28.9%);
· Place of stay during the studies: live at home 127 persons (62.3%), at dormitory 71 persons (34.8%), in lodgings 6 persons (2.9%);
· Family conditions: live with their families 160 persons (78.4%), with a life-partner or spouse 31 persons (15.2%), alone 7 persons (3.4%), with a friend 6 persons (2.9%).
According to the data presented above, most of the students had their secondary school leaving exams in Hungarian at vocational secondary schools, and the rate of those having applied for the full-time pre-school teacher training was high. A high proportion of the students took their exams in Hungary. It is important to remark that the J. Selye University is close to the Slovakian- Hungarian border, so students in Hungary can reach it easily. As for the parent's education level, the rate of those with vocational secondary education was high.
Results of Research
The development level of inductive cognition
The descriptive statistical indicators of the whole sample are summarized in Table 1. The best results were born in recognition of the analog (Task3) and the odd-one-out (Task2), while the weakest ones in the task required the recognition of regularities containing known operations (Task5). Concerning the latter, the difficulty was probably caused by the high level of memory burden since the results of certain operations had to be stored in the short-term memory and then to be modified with new operations and choose the correct final result from the available list; sensual – perceptual shifts must have caused trouble to the students. On the other hand, the students did not have enough time left for the last task because they consumed plenty of time for solving the first task, so they mapped out their time improperly, and the novel nature of the last task-induced difficulties as well.
Table 1.: Descriptive statistical indicators by tasks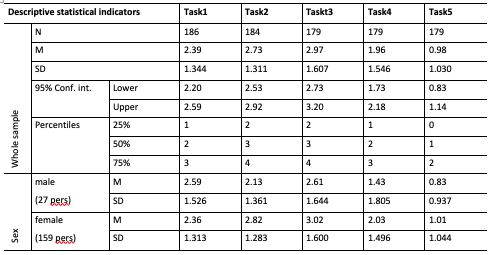

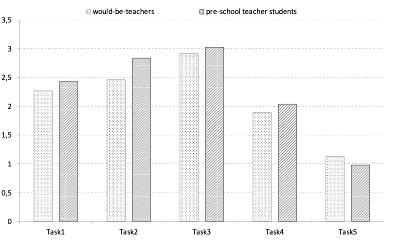
Figure 2: Average results of the certain tasks in terms of the two examined specializations
The students' results were compared by the various sub-samples, as well.
Except for the first one, females achieved better results, and as for the odd-one-out (Task2: Mann-Whitney U= 1348.500; p<0.05) and the recognition of regularities containing unknown operations (Task4: Mann-Whitney U= 1265.000; p<0.05), they reached significantly better results than men.
Correspondence students achieved better results for each task, except for the last one, in recognition of the odd-one-out elements (Task2: Mann Whitney U= 2542.500; p<0.05) and the analog (Task3: Mann Whitney U= 2795.000; p<0.05), they achieved significantly better results than full-time students.
Regarding the parents' educational level, the type of settlement where they lived, and the type of secondary school (grammar or vocational), any significant differences were not found in the averages of specific tasks. The same applies to the student's specialization and the country of the secondary school leaving exam (Hungary, Slovakia). However, it must also be remarked that the pre-school teacher students achieved better results (Figure 2) than their would-be-teacher peers, and so did those having taken their exams in Hungary as compared to those finishing their secondary school studies in Slovakia. However, these results cannot be generalized.
The results of the inductive reasoning test were summarized according to Figure 1: abstract reasoning, analog thinking, and diagrammatic thinking. The descriptive statistical indicators of these have been summed up in Table 2. Concerning abstract reasoning and considering the background variables, significant differences were found in terms of the student's specialization (Mann-Whitney U= 2598.500; p<0.05) and their place of stay during their studies (Mann-Whitney U= 2614.000; p<0.05). Correspondence students and those studying at home reached better results in each cognition component. In summary, it can be stated that the development level of the abstract and analog reasoning of these first-grade students was medium, while that of their diagrammatic thinking was weaker.
Table 2: Descriptive statistical indicators of inductive thinking and its components
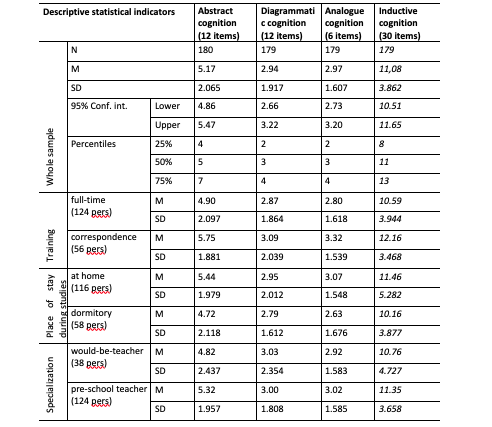
Pre-school teachers achieved better results than would-be teachers in each cognition component; however, these differences are insignificant.
The results of the 10 percent of students (17 persons) who had achieved the best (more than 16 points) were also evaluated in the inductive test separately. The cumulate diagram of the relative values of the part components is presented in Figure 3. The relative values of each of the three components fall between 0 and 1, thus cumulating them; the values between 0 and 3 are shown on the vertical axle. Only three students (H60, H114, and H162) have diagrammatic thinking at least as developed as the other two components. On the other hand, 6 students achieved the maximum result in the analog reasoning test, and their weaker result in the diagrammatic test debased their total performance (H61, H27, H175, H129, H3, H12).
Figure 3.: Rates of the components of inductive cognition at the students with the best results
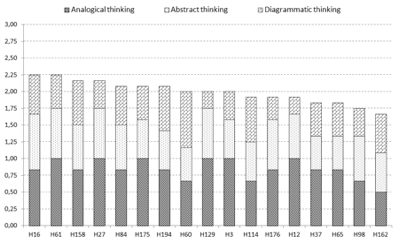
Relying on the analysis of the students' background variables with the best results, the following statements can be made. In this group of students, the proportion of
· those with a mother (29.4% vs. 15.2%) and father (23.5% vs. 9.8%) with a degree;
· women (94.1% vs. 82.4%);
· those living in a city (53.0% vs. 45.1%);
· having taken their school-leaving exams at grammar schools (47.1% vs. 38.7%) and
· taking their school-leaving exams in Hungary (52.9% vs. 40.7%) was higher.
However, no significant differences in specialization were found, the type of training, the place of stay during the studies, and the distance of the place of living from the university.
Time used for task solution
The second objective of this research was to analyze the time spent on solving the tasks and task items.
The students were given 1500 seconds to solve the tasks. Online measuring allowed to register the time spent on task solutions by items; thus, it became possible to analyze and compare them with the achieved results.
The first-grade would-be-teachers consumed the most time for solving the series continuation (Task1) and used the least time for the diagrammatic task containing unknown operations (Task4) (Figure 4). If these are compared to the data presented in Table 1, it can be stated that there is a correlation between the average results of certain task types and time consumption. However, high deviation rates imply considerable personal differences.
Figure 4.: Average and deviation of time spent on solving the certain task types
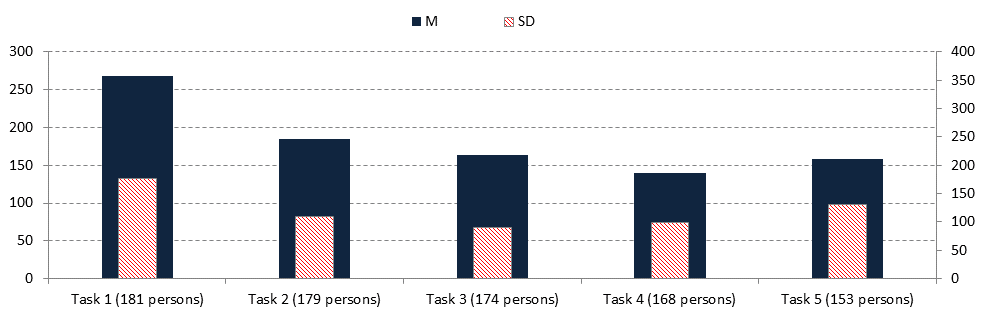
Remark: The left-hand vertical axle indicates the averages while the right one shows deviation.
If we focus on the first items, very diverse phenomena analyze the last task type, and the time consumption will also be found.
The items of the series continuation task (Task1) differed. However, the students understood the task relatively quickly, so time consumption reflects the difficulty level of the given item (Figure 5). It is also apparent that the more complex an item was (e.g., Task 1.4), the more significant personal differences could be observed, which is proved by high deviation values.
Figure 5: Average and deviation of the time spent on the series continuation items
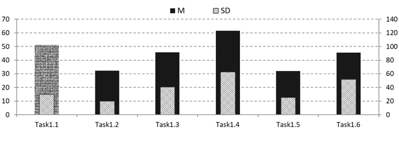
Remark: The left-hand vertical axle indicates the averages, while the right one shows deviation
Another phenomenon can be noticed regarding the diagrammatic items using general operations (Task5). According to Figure 4, the average time consumption of this task type almost agrees with that of the analog task (Task3). However, it can be seen that the first item meant a real challenge for the students (Figure 6), i.e., at first, they faced problems with understanding. Later this decreased gradually. Personal differences were less typical here, reflected by much more common deviation values; thus, it was equally difficult to solve the items for everyone in this case. As a result, students tended to rely on guessing rather than thinking thoroughly.
Figure 6: Average and deviation of the time used to solve the diagrammatic items containing known
operation
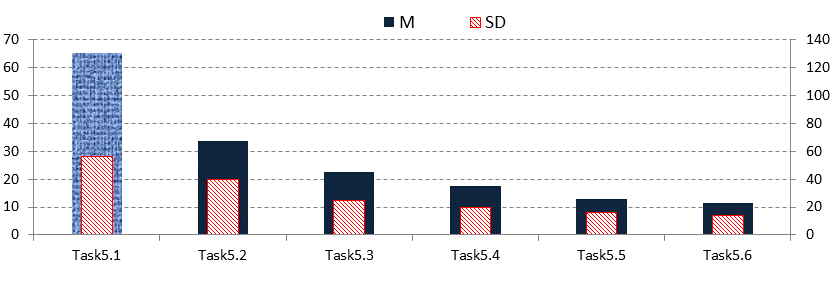
Remark: The left-hand vertical axle indicates the averages, and the right one shows deviation.
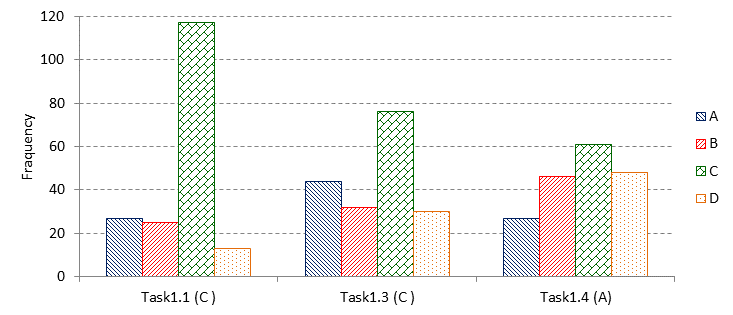
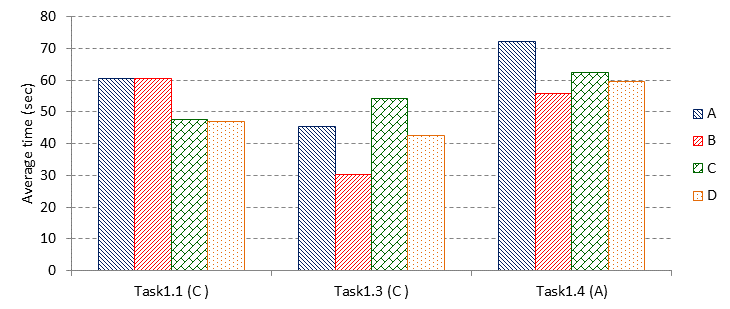
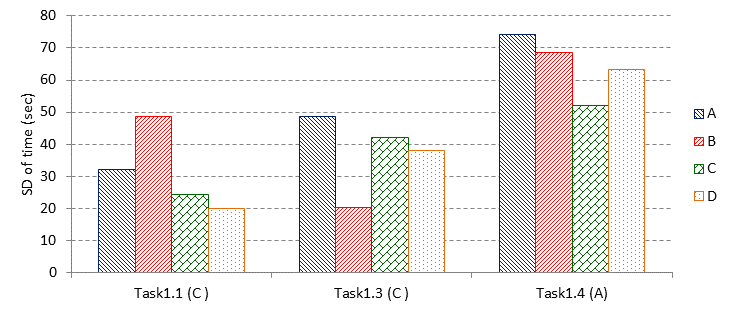
Returning to Figure 5, the online framework system allowed the analysis of the students' solutions to specific items. Three kinds of solutions were found for the series continuation task type (Figure 7). Task 1.1 was easy, and many of the students were able to solve it. Those choosing the correct answer (C) found the solution fast. The few who chose a lousy answer had spent a long time thinking about the solution. The solution of Task 1.3 shows more considerable divergence. The false solution B was chosen by many students, after a short time of thinking and with low personal differences (the good solution was C). Task1.4 proved to be rather tricky. Many chose false answers (B, C, D), with high time consumption and significant personal differences. The ones choosing the correct answer (A) used the most time for thinking, with considerable differences. The students giving the correct answer were also analyzed separately. 25 percent of the 27 students consumed less than 25 seconds to choose the correct answer, while 25 percent used more than 89 seconds. That someone solved this difficult task did not necessarily mean that he/she succeeded with the easier ones. There was only one student who managed to solve each of the 6 items without any mistakes. Most of them had 3 reasonable solutions for this task type. The descriptive statistical indicators of these students are significantly better than those presented in Table 1 (M= 3.44; SD= 1.155).
Time consumption in Task2 and Task3 was similar to that in Figure 5, while Task4 resembled Figure 6.
Concerning the background variables, significant differences were found in terms of gender and the type of training. Women spent significantly more time on solving Task2 (females: M= 169.85; SD= 101.801; males: M= 164.07; SD= 105.657; Mann-Whitney U=1348.500; p<0.05) and Task4 (females: M= 135.51; SD= 97.742; males: M= 101.53; SD= 79.097; Mann-Whitney U= 1265.000; p<0.05) than men. Correspondence student spent significantly more time on solving Task2 (correspondence students: M= 212.44; SD= 112.63; full-time students: M= 150.95; SD= 91.453; Mann-Whitney U= 2542.500; p<0.05) and Task3 (correspondence students: M= 194.49; SD= 70.356; full-time students: M= 137.90; SD= 90.079; Mann-Whitney U= 2795.000; p<0.05) than full-time students.
Figure 7.: Frequency of the series continuation items and mean and standard deviation of time consumption by items
Relation between the time used for task solution and inductive cognition
To explore the relationship between the amount of time used for task solutions and inductive reasoning, it was first based on the results of the best 27 students.
The students with the highest scores were ranked based on specific performance (Figure 8). 300 sec/point as the high specific performance was considered, which means that the students achieved a high number of points using little time. The values between 300 and 450 sec/point were assessed as specific performance of medium level, while the values above were considered low specific performance, i.e., a high amount of time was used to reach one unit of points.
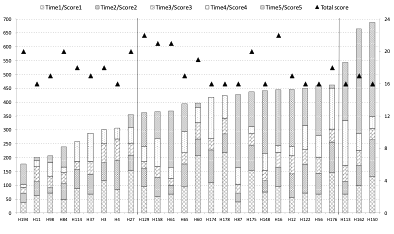
Figure 8 shows that in almost all cases (except for, e.g., H60, H11, or H176), the last task requiring diagrammatic thinking debased specific performance. However, there were also students who spent 4-5 minutes on this task, but they could solve any items from correctly (i.e. H37, H114, H4).
27 students were ranked according to the total scores gained in the five task types (Figure 9). It can be seen that the students, in most cases, utilized the whole time available; however, in each score category, there were one or two students who achieved results similar to the others' with little time consumption. For example, H11 or H87 in the 16-points group, H98 in the 17-points group, or H194 and H84 in the 20-points group.
Figure 8.: Specific performance of 27 students
Remark: The left-hand vertical axle indicates time and the right one shows the scores.
Figure 9.: Time consumption and total score of the 27 students
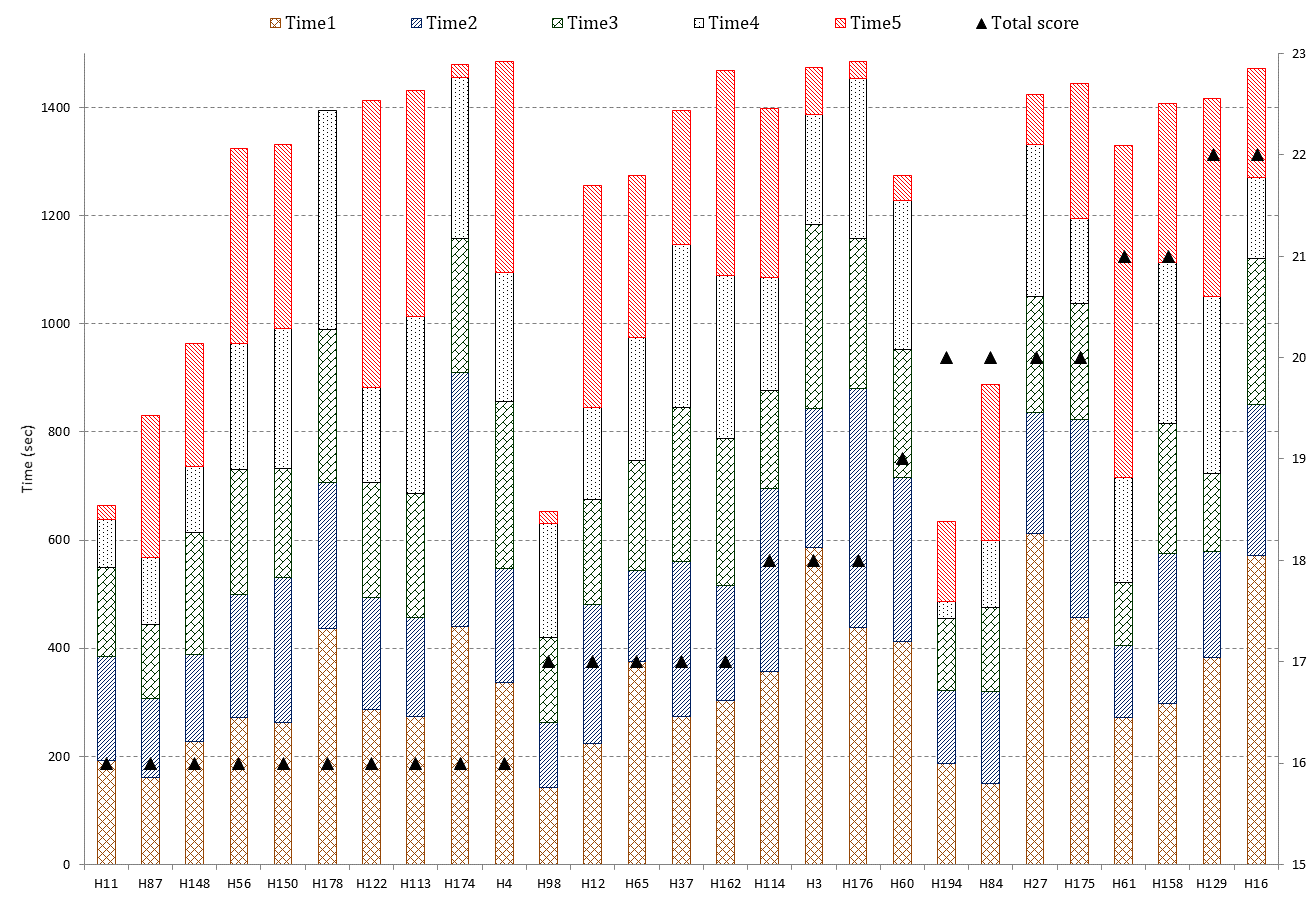
Figure 10.: Relation between time consumption and total score of the whole sample
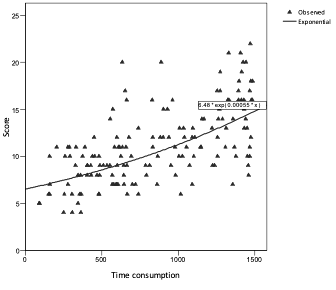
Figure 11.: Clusters composed in terms of the whole sample
It can be stated that the full utilization of the available time did not necessarily mean a high score; however, it is visible that each of the students, having reached more than 20 points, used almost entirely the 25 minutes available for the test.
The relation between time consumption and gained points was also examined in terms of the whole sample (Figure 10). The relation can be described sufficiently by an exponential function:
Score = 6.48*exp(0.00055*Time consumption)
The model accounts for 39.9% of all of the variances. The ANOVA test indicates a significant regressive relation (F=100.318; p<0.05).
Finally, a cluster analysis of the whole sample has been made. Clusters can be created according to the time used for the task solution. In this case, three groups can be created (Figure 11):
· "negligent "and superficial ones;
· considered but not persistent enough;
· persistent and diligent ones.
Each of the three groups contains students with low and high scores, as well; however, the tendency is what has been described by the regression analysis.
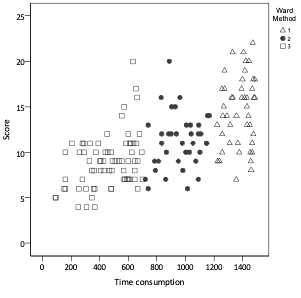
Reliability was checked by the K-means probe and was found satisfactory. The data of the cluster centroids are summarized in Table 3.
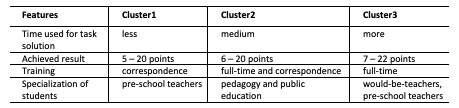
Background variables also examined the composition of the clusters in terms of the whole sample (Figure 12-13). A more significant rate of the full-time students belongs to Cluster3 while correspondence students belong to Claster1. Most would-be teachers are part of Cluster3, the ones in the pedagogy and public education program to Cluster2, while preschool teacher students mainly belong to Cluster1 and Cluster3. It was proved by the Khi-square probe that there was a significant correlation between the type of training and belonging to a cluster (F= 18.473; p<0.05) and between the program attended and belonging to a cluster (F= 15.138; p<0.05). Summarizing these, Table 4 presents the explanation of the clusters.
Table 3.: Cluster centroids and deviation
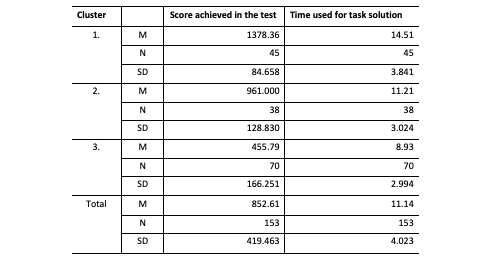
Figure 12.: Belonging to clusters by type of course
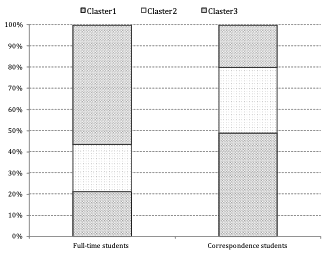
Figure 13.: Belonging to clusters by specialization
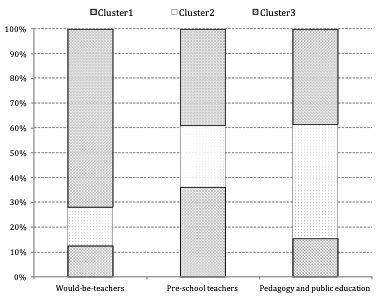
Table 4.: Explanation of clusters
Discussion
Competitiveness is an orienting notion that offers a pivot for the schools in preparing and developing their pupils. It reflects the strong demand for improving the economy and its impact that has extended competition to the world of education, making it clear that education is a direct competition factor. The competitive student is also successful in his/her school career and the labor market. I.e., he/she is someone who can find his/her place in a competitive world and can get on. Schools must provide the necessary bases for this. The question is what these bases are.
When responding to this question, one must return to one of the core problems of pedagogy: what is the relation between the school and the society like, and within that, the school and the economy? The answer seems evident: it is reasonable to describe competitiveness by the competencies in the cases of both the pupils and the teachers. Student competencies needed for labor market performance are primarily determined by economic aspects recently. This is reflected in the concepts and components of hard and soft skills. Thus the original question can be specified according to this: what should the learning material be, and how could the pupils' labor market key competencies be developed? This depends less on the concrete learning material and more on how the learning process is organized and what type of learning environment the pupil is surrounded by. So the primary stress is not put on WHAT to teach but HOW to. Moreover, this places teacher competencies in the limelight.
The educational methods applied during the lessons are affected by several factors, e.g., the characteristics of the subject, the type of the lesson (elaboration of new knowledge, practicing, summing up and systemizing or checking and evaluation of pupils' knowledge), the pupils' existing knowledge, their skills, age characteristics, etc. Solving this complex task system needs complex methodological competencies. For example, a would-be teacher should
· know the epistemological bases, cognition characteristics, logic, and terminology of the subject taught;
· know the inner characteristics of the subject as well as its cognition methods and the structure and inner logic of the educational material;
· be able to select and apply the methods and organizational forms developing the pupils' cognition, problem-solving, and cooperation skills;
· adapt the hubs, structure, and logic of transmission of the education material to the given student group and per the curricular rules and pedagogical objectives.
From the teacher's point of view, developing the pupils' soft skills needs hard methodological skills. Therefore, two preconditions of pupils' thinking, and within that inductive reasoning, should be mentioned here: the teacher's thinking should be as developed as possible, and (s)he should also possess the methodological competencies using the pupils' thinking and problem-solving skills can be developed.
For teacher training, this means a triple challenge. First, at the beginning of the training, it must be able to assess the development level of the students' cognition skills; their development must be given high priority during the training program; second and third, the teacher students must learn the methodology of developing pupils' cognition (Neubert & Binko, 1992; de Koning et al., 2002).
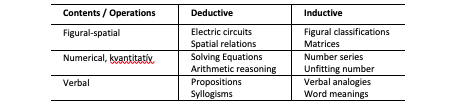
As for the structure of inductive cognition, there are five conceptions: 1) it is a general reasoning factor that bears several components both concerning its content (verbal, quantitative or numerical, figural-spatial) and operation (inductive, deductive). 2) Inductive and deductive reasoning are interrelated, however, with no content factor. 3) Deductive and inductive cognition processes cannot be separated from each other, while the three factors of reasoning: verbal, quantitative/numerical, and figural-spatial, are related. 4) It is a general reasoning factor with embedded and orthogonal content factors like verbal and quantitative reasoning but no figural-spatial factor. 5) Inductive and deductive reasoning are interrelated, including orthogonal content factors like verbal and quantitative reasoning but no figural-spatial factors (Wilhelm, 2005).
In the high-order model of fluid intelligence, Wilhelm (2005) used the measuring tool presented in Table 5 to examine reasoning in the dimensions of content and operation. The value of the correlation between fluid intelligence and the specific content components was very high (0.83-1.00), so any of the tests, but most of all the figural-spatial ones, were suitable to measure the development of thinking capacities.
Table 5.: High-order model of fluid intelligence (reasoning)
To assess the inductive thinking of first-grade would-be-teacher students, the figural test is applied in labor market aptitude tests (Newton & Bristol, n.s.), the model indicated in Figure 1. Future research will be worth examining the relation system of the two complex tests.
In Carroll's (1993) cognitive skills structure, cognition speed appears as one of the components of fluid intelligence. Applying Raven's Advanced Progressive Matrices (APM) test and the Test for Attentional Performance (TAP), Frank Goldhammer and Rinke H. Klein Entink (2011) found that (1) reasoning speed is a one-dimension construction that shows significant personal differences and that (2) cognition speed and reasoning capacity are in negative correlation but can clearly be distinguished. Regarding reasoning speed and thinking capacities, perceptual and executive attention differ as reasoning speed is only explained by executive attention while thinking capacities are accounted for by both covariants.
In this research, cognition speed was measured directly; however, in the future, it will be reasonable to extend the research beyond the area of attention to the field of visual perception, visual memory, and visuo-construction capacities, as well (pl. Benton Visual Retention Test). By doing so, this model will be possible to be described more precisely.
Conclusions and Implications
The research implemented at the Faculty of Education of the J. Selye University, Komarno, (Slovakia) involved 204 first-grade students. The research was aimed at the examination of the development level of the students' inductive thinking, and the following results can be made.
Development level of inductive cognition
The students achieved the best results in the analogue task and were the weakest in the diagrammatic task. The reason for the latter was probably the significant burden put on short-time memory (they had to store four medium states of four operations) and the frequent sensual–perceptual shifts.
Females achieved significantly better results concerning the odd-one-out task and the recognition of regularities containing unknown operations than males. At the same time, in the odd-one-out and the analog task correspondence, students performed significantly better than full-time students.
The development level of these first-grade students' abstract and analog thinking is medium, while their diagrammatic thinking is weaker.
The 10 percent of the students with the best results are women with parents with a degree; they live in cities and take their secondary school leaving exams in grammar schools in Hungary.
Time used for task solution
The first grade pedagogy students consumed the most time solving the series continuation and the diagrammatic task containing known operations, while they used the least time for the diagrammatic task containing unknown operations. There is a correlation between the average results of the specific task types and the time consumed.
The five task types can be divided into two groups based on analyzing the time used for the task solution. Each item of the two diagrammatic tasks proved equally difficult; several students only guessed. The time used for the items following each other showed a significantly decreasing tendency. However, as for the first three tasks, there were more manageable tasks demanding less time and more complex tasks requiring more time.
Females spent significantly more time finding the odd-one-out and the diagrammatic task containing unknown operations than men. In addition, correspondence students spent significantly more time finding the odd-one-out and the analog task than their full-time peers.
Relation between time consumption and inductive reasoning
The concept of specific performance has been introduced to demonstrate success, which was defined as the ratio of consumed time and the achieved score. This fraction indicates the speed of thinking, as well.
Utilization of the available time frame did not necessarily result in a high score; however, it could be observed that each student, having gained more than 20 points, utilized the 25 minutes given for the test almost entirely.
The relation between time consumption and the achieved score can be defined by an exponential function: Score = 6.48*exp(0.00055*Time consumption).
The cluster analysis was made in terms of the whole sample, and it was found that clusters could be created according to the time consumed for task solution: (a)" negligent" and superficial, (b) considered but not persistent enough, (c) persistent and diligent ones.
Acknowledgments
This research has been supported by the project titled "1/0117/19: Position, identity and education of minorities – societal self-realization strategies of the Hungarian minority in Slovakia.
References
· Alrawili, K. S., Osman, K., & Almuntasheri, S. (2020). Effect of scaffolding strategies on higher-order thinking skills in science classroom. Journal of Baltic Science Education, Journal of Baltic Science Education, 19(5), https://doi.org/10.33225/jbse/20.19.718;
· Baka, L. P. (2021). The Feminist Hungarian Folktale as Postmodern Combinatorics – The Analysis of Csenge Virág Zalka's Story-book Titled 'Ribizli a világ végén' [Currant at the end of the World]. AD ALTA: Journal of Interdisciplinary Research, 11(2), 18-24. www.doi.org/10.33543/1102;
· Balcar, J. (2014). Soft skills and their wage returns: Overview of empirical literature. Review of Economic Perspectives, 14(1), 3-15. https://doi.org/10.2478/revecp-2014-0001. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2488740;
· Bauman, Z. (2011). Modernità liquida. Gius, Laterza & Figli Spa, Roma-Bari. https://books.google.it/books?id=dSSODAAAQBAJ&printsec=frontcover&hl=it#v=onepage&q&f=false;
· Brewster, C., & Railsback, J. (2001). Supporting Beginning Teachers: How Administrators, Teachers, and Policymakers Can Help New Teachers Succeed. Northwest regional Educational Laboratory. Portland, OR. https://eric.ed.gov/?id=ED455619;
· Carneiro, P., Crawford, C., & Goodman, A. (2007). The impact of early cognitive and non-cognitive skills on later outcomes. London: Centre for the Economics of Education, London School of Economics. http://eprints.lse.ac.uk/19375/1/The_Impact_of_Early_Cognitive_and_Non-Cognitive_Skills_on_Later_Outcomes.pdf;
· Carnevale, A. P. (2013). 21st century competencies: For College and Career Readiness. National Career Development Association, Broken Arrow. https://repository.library.georgetown.edu/bitstream/handle/10822/559289/CD_21stCenturyCompetencies.pdf?sequence=1&isAllowed=y;
· Carnochan, S., Taylor, S., Pascual, G., & Austin, J. M. (2014). Employer Perspectives on the Role of Soft Skills in Subsidized Employment Relationships. In: Families in Society: The Journal of Contemporary Human Services 95(3), 187-194. https://doi.org/10.1606/1044-3894.2014.95.24;
· Carroll, J. B. (1993). Human cognitive abilities: A survey of factor-analytic studies. Cambridge Univesity Press. https://doi.org/10.1017/CBO9780511571312;
· Cinque, M. (2016). „Lost in translation“. Soft skills development in European countries. Tuning Journal for Higher Education. 3(2), 389-427 http://www.tuningjournal.org. https://www.researchgate.net/publication/303770318_Lost_in_translation_Soft_skills_development_in_European_countries [accessed Aug 18 2020];
· Cornalli, F. (2018). Training and developing soft skills in higher education. 4th International Conference on Higher Education Advances (HEAd’18). Universitat Politecnica de Valencia, Valencia. http://dx.doi.org/10.4995/HEAd18.2018.812. [accessed Aug 18 2020];
· Csapó, B. (1997). The development of inductive reasoning: cross-sectional assessments in an educational context. International Journal of Behavioral Development, 20(4), 609-626. https://doi.org/10.1080/016502597385081. https://www.researchgate.net/publication/236016451_The_Development_of_Inductive_Reasoning_Cross-_sectional_Assessments_in_an_Educational_Context
· Csehiová, Á., & Kanczné Nagy, K. (2019). Élmény-foglalkozások a Selye János Egyetemen "MŰvészet-PEdagógia-PSZIchológia". (Edutainment classes at J. Selye University. Arts-Pedagogy-Psychology) In 11th International conference of J. Selye University: Pedagogical sections. Komárno: J. Selyeho University, 2019. pp. 9-17. https://doi.org/10.36007/3334.2019.09-17;
· Csehiová, A, Kanczné Nagy, K., & Tóth-Bakos, A. (2020). Experience Education to Alleviate Fears of Educator Candidates in their University Studies. AD ALTA: Journal of Interdisciplinary Research, 10(2), 170-175. www.doi.org/10.33543/1002;
· Demetriou, A., Spanoudis, G., & Mouyi, A. (2011). Educating the developing mind: Towards an overarching paradigm. Educational Psychology Review, 23(4), 601–663. https://doi.org/10.1007/s10648-011-9178-3.;
· de Koning, E., Hamers, J. H. M., Sijtsma, K. & Vermeer, A. (2002). Teaching Inductive Reasoning in Primary Education. Developmental Review, 22(2), 211-241, https://doi.org/10.1006/drev.2002.0548;
· Eger, H., & Grossmann, V. (2004). Noncognitive Abilities and Within-Group Wage Inequality. Institute for the Study of Labour, Bonn. http://ftp.iza.org/dp1024.pdf;
· Engler, Á. (2019): Non-traditional students in higher education. Hungarian Educational Research Journal, 9(3), 560-564. https://eera-ecer.de/ecer-programmes/conference/24/contribution/47384/;
· Flores, M. A., & Day, Ch. (2006). Contexts which shape novice teachers’ identities: A multi-perspective study. Teaching and Teacher Education, 22(2), 219-232. https://doi.org/10.1016/j.tate.2005.09.002;
· Georgiev, N. (2008). Item Analysis of C, D and E Series from Raven’s Standard Progressive Matrices with Item Response Theory Two-Parameter Logistic Model. Europe’s Journal of Psychology, 4(3), https://ejop.psychopen.eu/index.php/ejop/article/view/431/html;
· Goldhammer, F. & Klein Entink, R. H. (2011). Speed of reasoning and its relation to reasoning ability. Intelligence, 39(2-3), 108-119. https://doi.org/10.1016/j.intell.2011.02.001;
· Gordon, G. (2003). University Roles and Career Paths: Trends, Scenarios and Motivational Challenges. Journal of Higher Education Policy and Management. 15(3), 25-25. https://www.researchgate.net/publication/227461495_University_Roles_and_Career_Paths_Trends_Scenarios_and_Motivational_Challenges;
· Goswami, U. (1991). Analogical reasoning: what develops? A review of research and theory. Child Development, 62(1), 1-22. https://doi.org/10.1111/j.1467-8624.1991.tb01511.x ;
· Hamers, J. H. M, Koning, de E. & Sijtsma, K. (2000). Inductive reasoning in the third grade: intervention promises and constraints. Contemporary Educational Psychology, 23(1), 132-148. https://research.tilburguniversity.edu/en/publications/inductive-reasoning-in-third-grade-intervention-promises-and-cons;
· Haselberger, D., Oberhuemer, P., Pèrez, E., Cinque, M., & Capasso D. (2012). Mediating Soft Skills at Higher Education Institutions Guidelines for the design of learning situations supporting soft skills achievement. Handbook of the ModES project: Lifelong learning programme. Education and Culture DG Lifelong Learning Programme, European Union. http://www.euca.eu/en/prs/modes-handbook.aspx;
· Hattie, J. A. C. (2003). Teachers Make a Difference, What is the research evidence? Paper presented at the Building Teacher Quality: What does the research tell us. ACER Research Conference, Melbourne, Australia. http://research.acer.edu.au/research_conference_2003/4/
· Heckman, J., & Kautz, T. (2012). Hard Evidence on Soft Skills. Labour Economics. 19(4), 451–464. http://www.nber.org/papers/w18121;
· Holmes, G. (2002). What is called thinking? The Journal of Critical Psychology, Counselling and Psychotherapy, 2(1), 33-39. https://www.researchgate.net/publication/309395268_What_is_called_thinking;
· Jacobs, P. I., & Vandeventer, M. (1968). Progressive Matrices: An experimental, developmental, nonfactorial analysis. Perceptual and Motor Skills. 27(3), 759-766. https://doi.org/10.2466%2Fpms.1968.27.3.759;
· Kane, H., & Brand, Ch. (2003). The importance of Spearman’s g. As a psychometric, social, and educational construct. The Occidental Quarterly, 3(1), 7-30. https://www.toqonline.com/archives/v3n1/TOQv3n1Kane-Brand.pdf;
· Kautz, T., Heckman, J. J., Diris, R., Weel, B., & Borghans, L. (2014). Fostering and measuring skills: Improving cognitive and non-cognitive skills to promote lifetime success. Directorate for Education and Skills. Centre for Educational Research and Innovation (CERI). http://www.oecd.org/education/ceri/Fostering-and-Measuring-Skills-Improving-Cognitive-and-Non-Cognitive-Skills-to-Promote-Lifetime-Success.pdf;
· Kechagias, K. (2011). Teaching and Assessing Soft Skills. Thessaloniki: 1st Second Chance School of Thessaloniki. http://research.education.nmsu.edu/files/2014/01/396_MASS-wp4-final-report-part-1.pdf;
· Klauer, K. J. (1999). Fostering higher order reasoning skills: The case of inductive reasoning. In Hamers, J. H. M., Luit van J. E. H., & Csapó, P. (1999). Teaching and learning thinking skills. Lisse: Swets & Zeitlinger. pp. 131–156. https://publications.rwth-aachen.de/record/86563;
· Klauer, K. J., & Phye, G. D. (2008). Inductive Reasoning: A Training Approach. Review of Educational Research, 78(1), 85-123. https://doi.org/10.3102/0034654307313402;
· Knight, P., & Page, A. (2007). The Assessment of “Wicked” Competences. Report to the Practice Based Professional Learning Centre, 2007, http://www.open.ac.uk/opencetl/sites/www.open.ac.uk.opencetl/files/files/ecms/web-content/knight-and-page-(2007)-The-assessment-of-wicked-competences.pdf;
· Kozma, T., & Pusztai, G. (2018): A Coleman-jelentés hatása Magyarországon a rendszerváltás előtt és után. (The impact of the Coleman report in Hungary before and after the change of regime.) In: Tóth, D. A. (szerk.): Az oktatás gazdagsága. Tanulmányok Polónyi István tiszteletére. CHERD.H. Debrecen. 2018. pp. 25-49. http://www.elib.hu/18700/18743/18743.pdf;
· Lukovics, M., & Zuti, B. (2014). Egyetemek a régiók versenyképességének javításáért: „negyedik generációs” egyetemek? (Universities for improving the competitiveness of regions: “4th generation” universities?) Tér és Társadalom. Space and Society. 28. (4), 77-97. https://doi.org/10.17649/TET.28.4.2587;
· Mackintosh, N. J. (1998). IQ and human intelligence. Oxford University Press, Oxford. https://www.amazon.com/IQ-Human-Intelligence-Nicholas-Mackintosh/dp/0199585598;
· Manpower Group (2015). Talent Shortage Survey Research Results. Manpower Group, Milwaukee. https://www.manpowergroup.com/wcm/connect/2d7acf6d-2814-489a-bd7f-ec5c98d67481/2013_Talent_Shortage_Survey_Results_US_high%2Bres.pdf?MOD=AJPERES&CACHEID=ROOTWORKSPACE-2d7acf6d-2814-489a-bd7f-ec5c98d67481-n2AdFwM;
· Meacham, S., Phalp, K., Ross, M., & Udall. M. (2014). The “New” Soft Skills for Employability. ICICTE 2014 Proceedings, pp. 361-368. file:///C:/Users/USER/Downloads/9.5Meacham.pdf;
· Molnár, Gy., Greiff, S., & Csapó, B. (2013). Inductive reasoning, domain specific and complex problemsolving: Relations and development. In: Thinking Skills and Creativity. Volume 9 (2013), 35– 45. https://doi.org/10.1016/j.tsc.2013.03.002;
· Moss, P. I., & Tilly, Ch. (2001). Stories employers tell: Race, skill, and hiring in America. New York: Russell Sage Foundation. https://www.amazon.com/Stories-Employers-Tell-Multi-City-Inequality/dp/0871546329;
· Mousa, M. (2017). The Influence of Inductive Reasoning Thinking Skill on Enhancing Performance. International Humanities Studies. 4(3), 37-48. https://www.researchgate.net/publication/319472191_The_Influence_of_Inductive_Reasoning_Thinking_Skill_on_Enhancing_Performance;
· Neubert, G. A. & Binko, J. B. (1992). Inductive reasoning in the secondary classroom. pp. 128. Washington: National Education Association of theUnited States Aspects Learning.
· Newton, P., & Bristoll, H. (n.s.). Numerical reasoning, verbal reasoning, abstract reasoning, personality tests. Psychometric Success. https://www.psychometric-success.com/;
· Pachauri, D., & Yadav, A. (2012). Importance of Soft Skills in Teacher Education Programme. International Journal of Educational Research and Technology. 5(1), 22-25. http://soeagra.com/ijert/ijertmarch2014/5.pdf;
· Pásztor, Á. (2019). Induktív és kombinatív gondolkodás fejlettségének online vizsgálata. (An online study of the development of inductive and combinatorial thinking.) Iskolakultúra, 29(1), 42 – 54. https://doi.org/10.17543/ISKKULT.2019.1.42.;
· Pellegrino, J. W., & Glaser, R. (1984). Analyzing aptitudes for learning: inductive reasoning. Lerning Research and Development Center. University of Pittsburg. https://files.eric.ed.gov/fulltext/ED243781.pdf;
· Pellerey, M. (2017). Soft skill e orientamento professionale. www.cnos-fap.it/sites/default/files/pubblicazioni/soft_skill.pdf;
· Orlando de, P., & Altomari, N. (2019): A Tool to Measure Teachers’ Soft Skills: Results of a Pilot Study. Advances in Social Science and Culture. 1(2). https://doi.org/10.22158/assc.v1n2p245. https://www.researchgate.net/publication/338048900_A_Tool_to_Measure_Teachers'_Soft_Skills_Results_of_a_Pilot_Study;
· Pisoňová, M. (2017). Implementation of motivational strategies between head teachers and foreign language teachers. Journal of Language and the Cultural Education. 5(1), 127-144. https://doi.org/10.1515/jolace-2017-0008 . https://content.sciendo.com/configurable/contentpage/journals$002fjolace$002f5$002f1$002farticle-p127.xml;
· Plumert, J. M. (2008). Children's Thinking is not Just about What is in the Head: Understanding the Organism and Environment as a Unified System. Advances in Child Development and Behavior. Volume 36, 373-417. https://doi.org/10.1016/S0065-2407(08)00009-8;
· Prasad, B., & Nagendra, B. (2017). Soft Skills for Enhancing Employability. International Journal of Managerial Studies and Research. 5(11), 17-21. http://dx.doi.org/10.20431/2349-0349.0511003;
· Rashidi, R. A. M., Zaihan, N. A., & Samat, M. F. (2018). Developing soft skills student´s through co-curriculum activity: A case study of UiTM Cawangan Kelantan. Konvensyen Kebangsaan Pemimpin Pelajar. https://www.researchgate.net/publication/329388813_Developing_soft_skills_in_students_through_co-curriculum_activity_a_case_study_of_UiTM_Cawangan_Kelantan;
· Resing, W. C. M. (1993). Measuring inductive reasoning skills: The construction of a learning potential test. In Hammers, J. H. M., Sijstma, K., & Ruijssenaars, A. J. J. M. (ed.). Learning potential assessment. Theoretical, methodological and practical issues. Amsterdam: Swets and Zeitlinger. pp. 219–242.;
· Resnick, L. B. (1987): Education and Learning to Think. National Academy Press, Washington. Committee on Research in Mathematics, Science, and Technology Education. http://www.nap.edu/catalog/1032.html;
· Robles, M. M. (2012). Executive perceptions of the top 10 soft skills needed in today‘s workplace. Business Communication Quarterly, 75(4), 453-465. https://doi.org/10.1177/1080569912460400;
· Salleh, K. M., Sulaiman, N. L., & Talib, K. N. (2010). Globalization's Impact on Soft Skills Demand in the Malaysian Workforce and Organizations: What makes graduates employable? Proceedings of the 1 st UPI International Conference on Technical and Vocational Education and Training. Bandung, Indonesia. https://www.academia.edu/490093/Globalizations_Impact_on_Soft_Skills_Demand_in_the_Malaysian_Workforce_and_Organizations_What_makes_graduates_employable;
· Söderquist, S., Nutley, S. B., Ottersen, J., Grill, K. & Klinberg, T. (2012). Computerized training of non-verbal reasoning and working memory in children with intellectual disability. Frontiers in Human Neuroscience. 6. 271-279. https://www.researchgate.net/publication/232236938_Computerized_training_of_non-verbal_reasoning_and_working_memory_in_children_with_mental_retardation;
· Spearman, C. (1927). The Abilities Of Man their Nature And Measurement. Nature 120, 181–183 (1927). https://doi.org/10.1038/120181a0;
· Stanovich, K. E., Toplak, M. E., & West, R. F. (2008). The Development of Rational Thought: A Taxonomy of Heuristics and Biases. Advances in Child Development and Behavior 36, pp. 251-285. https://doi.org/10.1016/S0065-2407(08)00006-2.;
· Sternberg, R. J. (1985). Beyond IQ: A Triarchic Theory of Intelligence. Cambridge University Press, New York. https://books.google.sk/books?id=jmM7AAAAIAAJ&printsec=frontcover&hl=sk&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false;
· Sternberg, R. J., & Ben-Zeev, T. (Eds.) (1996). The nature of mathematical thinking. (Studies in Mathematical Thinking and Learning Series). Lawrence Erlbaum, Mahwah. https://www.amazon.com/Nature-Mathematical-Thinking-Studies-Learning/dp/0805817999;
· Svecnik, E. (2008). The Integration of Transversal Competences in Classroom Instruction at Secondary Level I. In: A toolkit for the European citizen - The implementation of Key Competences. Challenges and opportunities. 2008 CIDREE/DVO. pp. 61-75. http://www.cidree.org/fileadmin/files/pdf/publications/YB_8_A_Toolkit_for_the_European_Citizen.pdf;
· Tang, K. N. (2013). Teaching as collective work: What are the needs of novice teachers? 3rd World Conference on Learning, Teaching and Educational Leadership. Procedia Social and Behavioral Sciences, 93, 195-199. https://core.ac.uk/download/pdf/82516727.pdf;
· Tang, K. N., Yie, C. S., & Shahid, S. A. M. (2015a). Quality teaching: Relationship to soft skills acquisition. Procedia-Social and Behavioral Sciences, 191, 1934-1937. https://doi.org/10.1016/j.sbspro.2015.04.204. https://www.researchgate.net/publication/282536112_Quality_Teaching_Relationship_to_Soft_Skills_Acquisition;
· Tang, K. N., Hashimah, M. Y. & Hashim N. H. (2015b). Soft Skills Integration in Teaching Professional Training: Novice Teachers’ Perspectives. 5th World Conference on Learning, Teaching and Educational Leadership, WCLTA 2014. Procedia - Social and Behavioral Sciences. 186 (2015) pp. 835-840. https://www.sciencedirect.com/science/article/pii/S1877042815024647 ;
· Tang, K. N., Ching, S. Y., & Mohd, S. A. (2015c). Quality teaching: Relationship to soft skills acquisition. Procedia-Social and Behavioral Sciences, 191, pp. 1934-1937. https://doi.org/10.1016/j.sbspro.2015.04.649;
· Tang, K. N., (2018). The importance of soft skills acquisition by teachers in higher education institutions. Kasetsart Journal of Social Sciences. (2018), pp. 1-6. DOI: 10.1016/j.kjss.2018.01.002
· Verma, S. (2013). Enhancing employability @ soft skills. Pearson Education India. https://books.google.sk/books/about/Enhancing_Employability_Soft_Skills.html?id=QoMzF6_FOWYC&redir_esc=y;
· Veroszta, Zs., & Nyüsti, Sz. (2015). Institutional effects on Bachelor-Master-level transition. International Journal of Social Sciences, 4(1), pp. 39-61. https://www.iises.net/download/Soubory/IJOSS/V4N1/pp38-61_ijossV4N1.pdf;
· Vodegel Matzen, L. B. L., Molen van der, M. W., & Dudink, A. C. M. (1994). Error analysis of Raven test performance. Personality and Individual Differences, 16(3), 433-445. https://doi.org/10.1016/0191-8869(94)90070-1;
· Wilhelm, O. (2005). Measuring reasoning ability. In O. Wilhelm & R. W. Engle (Eds.), Handbook of Understanding and measuring intelligence (pp. 373-392). London: SAGE Publications Ltd. https://doi.org/10.4135/9781452233529.n21;
· Winch, Ch. (1990). Language, ability and educational achievement. Routledge, London. https://doi.org/10.4324/9781315530970;
· Wu, B. (2011). Consumption and Management. New Discovery and Applications. Chandos Publishing. 510 p. https://doi.org/10.1016/C2013-0-18142-1.