DOBÁK Dávid – CSUTA Ákos – MEGYERI Krisztina – SZILÁGYI Brigitta

A geometriai gondolkodás szintjeinek feltérképezése a van Hiele-elmélet segítségével

Bevezetés

Szerte a világban számos kutatás született és születik, amelyek feltérképezik a középiskola-egyetem átmenet nehézségeit. Sokan dolgoznak azon, miként lehetne ezt a szakadékot könnyebben áthidalhatóvá tenni, csökkentve ezáltal a lemorzsolódást, amely különösen a STEM területeken magas még azokban az országokban is, ahol valamiféle felvételi eljárást követően kerülnek a diákok a választott szakra.

A magyar felsőoktatásban matematikából jellemző gyakorlat, hogy az elsőéves hallgatóknak dolgozatot kell írniuk, amellyel ellenőrzik, hogy rendelkeznek-e a tanulmányok megkezdéséhez szükséges ismeretekkel. A többnyire az első héten megírt dolgozat adott szinten való teljesítése több szakon a kalkulus tárgy elvégzésének szükséges feltétele. Sikertelen dolgozat esetén több felsőoktatási intézményben a hallgatók számára felzárkózási lehetőséget biztosítanak a középiskolai ismereteket felelevenítő kurzussal. Ez mindenképpen hasznos, noha nem könnyű a diáknak azzal szembesülni, hogy még el sem kezdődött igazán a szemeszter, már kudarcot vallott. Vannak olyan egyetemek is, ahol ilyen mérésre nem kerül sor. Ebben az esetben megvan a veszélye annak, hogy a többnyire a szemeszter közepén esedékes első zárthelyi elérkezésekor a diák lemaradása a kezdeti feltételek elégtelensége miatt már olyan tetemes, hogy borítékolható a sikertelenség.

A probléma Európa más országaiban is ismeretes, Braun és munkatársai egy lehetséges megoldást ismertetnek[1]. Jelen munka egy másik, ugyancsak hasznos gyakorlatot ismertet, amely egy bemeneti teszttel segíti az elsőéves hallgatók matematikai gondolkodásának feltérképezését.

Milyen tesztet érdemes végezni? Ha az adott szak nem követel meg emelt szintű érettségit, akkor a bemenő teszt sem haladhatja meg a középszint ismeretanyagát. De vajon az ismeretek mérése elegendő-e? Bizonyos rutin eljárások meglétének ellenőrzése egy-egy bemenő teszten abban mindenképpen segítségünkre lehet, hogy a legproblémásabb eseteket kiszűrjük. Az ilyen mérések azonban nem adnak felvilágosítást arról, hogy a begyakorolt eljárásokon túl a diák birtokában van-e egy olyan matematikai érettségi szintnek, ami lehetővé teszi számára az egyetemi axiomatikus felépítésű anyag megértését, az ott szerzett ismeretek szaktárgyakban való alkalmazását. Azonban van mód arra, hogy megvizsgáljuk, milyen gondolkodási szinten vannak diákjaink, hogy lássuk, a matematikai gondolkodás folyamatának mely állomásánál járnak és hogy az adott  állapotból van-e lehetőség az egyetemi tananyag elsajátítására vagy először a megfelelő szint elérését kell megvalósítani. Egy ilyen mérés arról is tájékoztat, honnan kell tovább vinni a hallgatókat, hasznos információkat nyerhetünk a fejlesztést, felzárkóztatást illetően.

Mivel a geometriai és a logikus, elemző gondolkodás erős kapcsolatot mutatnak, érdemes egy a nemzetközi gyakorlatban is elterjedt van Hiele-elméleten alapuló tesztet alkalmazni. Ennek segítségével választ kaptunk kutatásunk fő kérdésére, hogy a Budapesti Corvinus Egyetem elsőéves emberi erőforrás szakos hallgatói a felsőfokú tanulmányaik sikeres teljesítéséhez szükséges megértési szinten vannak-e.

Dina van Hiele-Geldof és Pierre van Hiele az 1950-es években dolgozták ki a geometria megértésének szintjeit. Bruner elmélete szerint minden életszakasznak megvannak a fejlődési szintjei ([2], [3], [4]). Ezek a szintek egymásra épülnek, egy diák nem juthat el egy felsőbb szintre az összes korábbi szint birtoklása nélkül. Ez egy olyan szempont, amire mind a felzárkóztatásnál, mind pedig a tananyag felépítésénél tekintettel kell lennünk.

Az eredményes tanítás szükséges feltétele, hogy ismerjük azt, milyen szinten vannak a diákjaink és igyekezzünk őket minél magasabb szintre juttatni. A különböző megértési szinten lévő diákok nehezen vagy egyáltalán nem értik meg egymást, nem képesek elfogadni a másik szinten lévő társuk érveléseit. Egy alsóbb szinten lévő diák fölöslegesnek gondolhatja a fölsőbb szinten lévő indoklását, mert nem érzi szükségesnek, hogy állításait külön alátámassza, számára azok teljesek. Ezzel szemben a fölsőbb szinten lévő nem tekinti teljes értékű indoklásnak az alsóbb szintű által adott magyarázatot. A tanulócsoportok, egyetemi tankörök kialakításakor jó, ha figyelembe vesszük ezt. Azon ismeretek birtokában, hogy ki milyen gondolkodási szinten van, könnyebben valósíthatunk meg differenciált oktatást is.

Adat és módszer

A holland didaktikus házaspár a matematikán belül a geometria megértésének szintjeit dolgozta ki részletesebben. Az elmélet állításainak igazolására később több tanulmány is született ([5], [6], [7], [8]). Az 1980-as években született meg a legismertebb teszt, amely ezeket a szinteket hivatott mérni és a közoktatás szerkezete miatt a magyar hallgatók mérésére jól alkalmazható, ezért mi is ezt használtuk ([8]).

Az Usiskin-féle feladatsor 25 kérdésből áll, 5 egymásra épülő kompetenciát mér és minden kompetenciát 5 kérdés hivatott mérni. A kérdések tesztfeladatok, öt válaszlehetőségből pontosan egy helyes. Életkortól, iskolai végzettségtől függetlenül 35 perc áll rendelkezésre a megoldáshoz. A teszt eredménye alapján a kitöltő vagy besorolható valamelyik van Hiele szintbe, vagy lehet nem besorolható is. A besorolhatók szintje 0, 1, 2, 3, 4 vagy 5 lehet, 0 jelenti a kompetenciák teljes hiányát, 5 pedig a legmagasabb szintű kompetencia meglétét.

A szintek a következő képességet birtoklását jelentik:

1. szint: A személy képes alakzatok felismerésére. Az alakzatot megjelenése alapján érzékeli. Részleteit, tulajdonságait nem képes megfigyelni; enélkül az összefüggések megértésére még nem képes. Például felismeri, hogy az alakzat négyzet, de annak téglalap voltát nem képes megállapítani.

2. szint: A személy az alakzatokat már annak tulajdonságaival képes azonosítani. Például tudja, hogy egy négyszög, amelynek szögei derékszögek, téglalap, azonban még nincs olyan mértékű tudás birtokában, hogy a téglalapok és négyzetek halmaza közötti relációt megértse.

3. szint: A személy az alakzatokat annak definíciójával azonosítja, ezáltal képessé válik például annak felismerésére, hogy a négyzet egyben téglalap is. Ezenfelül megért egyszerűbb bizonyításokat, képes érvelni, bizonyítási lépést elvégezni.

4. szint: A személy ismeri az axiómarendszer jelentését, az axiómák és az állítások, definíciók közötti különbséget, de nem feltétlen tudja visszavezetni bizonyítását axiómákra. Le tud vezetni állításokat, de „nyilvánvalónak tűnő” állításokat nem érzi, hogy bizonyítania kellene. Például ha egy egyenesre merőleges egyenesre merőleges egy harmadik egyenes, akkor első és harmadik egyenes párhuzamosságát bizonyítás nélkül nyilvánvalónak érzi. Szükségtelennek látja a következmények igazolását is.

5. szint: A személy absztrakt gondolkodásra képes. Képes a leggyakrabban használtan túl más axiómarendszerrel is dolgozni, így például képes nem euklideszi geometriát használni. Ezt a szint a legmagasabb a van Hiele-rendszerben, általában csak kivételes tehetségű személyek képesek elérni (középiskolában: többnyire speciális matematika tagozatra járók, felsőoktatásban: matematikai, műszaki hallgatók).

A teszt rövidített leírása a [8] forrás alapján készült, illetve a szintek teljes meghatározásai is elolvashatók itt.

A van Hiele-elmélet szerint csak akkor tudhatja magáénak valaki egy adott szinthez tartozó kompetenciát, ha birtokában van a szintet megelőző összes kompetenciának is. Például, ha valaki a teszt során teljesítette az 1-es, 2-es, 3-as és 4-es szintekhez tartozó kritériumot, akkor az ő szintje 4-es, viszont, ha valaki teljesítette az 1-es, 2-es és 4-es szintekhez tartozó kritériumot, de a 3-as szinthez tartozót nem, akkor ő nem sorolható egyik szinthez sem, mert a négyes szinthez teljesítenie kellett volna a hármas szintet is (annyit azonban elmondhatunk róla, hogy a van Hiele szintje eléri a kettőt). A továbbiakban az ilyen nem besorolható személyekre a „not fit” kifejezéssel hivatkozunk.

A teszt kiértékelése kétféleképpen történhet: az egyik szerint akkor van birtokában a kitöltő egy szinthez tartozó kompetenciának, ha az adott kompetenciára vonatkozó 5 feladatból legalább hármat old meg helyesen (továbbiakban megengedő van Hiele), a másik módszer esetén ez a szám 4 (továbbiakban szigorú van Hiele). 

A Nemzeti Alaptanterv (NAT) által meghatározott fejlődési folyamat jól megfeleltethető a van Hiele-elméletben definiált gondolkodási szinteknek. Ez lehetővé teszi a van Hiele-típusú tesztek alkalmazását a magyar köz- és felsőoktatásban tanuló diákok esetén. Az első szint a 4. osztályos, a második szint a 6. osztályos, a harmadik szint a 8. osztályos, a negyedik szint (a bizonyítás szintje) pedig a 12. osztályos követelményrendszernek felel meg. Azt mondhatjuk tehát, hogy az általános iskolát elvégezve a harmadik, középiskola végére pedig a negyedik van Hiele szintre kellene eljutniuk a tanulóknak a NAT előírásai szerint. Ez elméletileg összhangban van a felsőoktatás igényeivel. Kutatásunkban választ adunk arra, hogy teljesül-e ez a gyakorlatban is.

A teszt Usiskin-féle verziója elektronikus formában, az EduBase online oktatási portál használatával került megírásra. A tesztet 98 elsőéves, emberi erőforrás szakos hallgató töltötte ki, közülük 76 nő, 22 férfi volt. Ők egy jellemzően magas felvételi ponthatárokkal (400 feletti) rendelkező egyetem elsőéves hallgatói voltak. A vizsgált szakon a felvételi ponthatár meghaladja a 430 pontot, ami magasnak számít a magyar, maximum 500 pontos felvételi rendszerben. A hallgatóknak csak egy csekély hányada érettségizett emelt szinten matematikából, többen azonban jártak matematika fakultációra, tehát 11. és 12. osztályban heti öt órában tanulták a matematikát. A fakultációra járók megismerkedhettek a differenciál- és integrálszámítás alapjaival, számukra az első féléves egyetemi matematika tananyag nagyon sok ismerős elemet tartalmaz. A matematikát középszinten tanulók azonban nincsenek könnyű helyzetben az egyetemen, mert nagyon gyorsan nagyon sok új fogalommal kell megismerkedniük és azokat a szakmai tárgyakban biztonsággal használniuk.

Eredmények

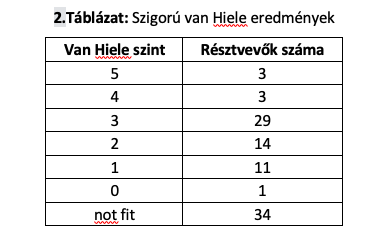
A 98 kitöltő eredményeinek megoszlása megengedő értékeléssel az 1. táblázatban látható, míg a szigorú értékeléssel kapott eredményeket a 2. táblázat mutatja.

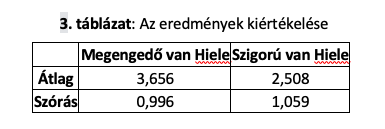
A két különböző számítással kapott eredmények átlaga és szórása a 3. táblázatban található.

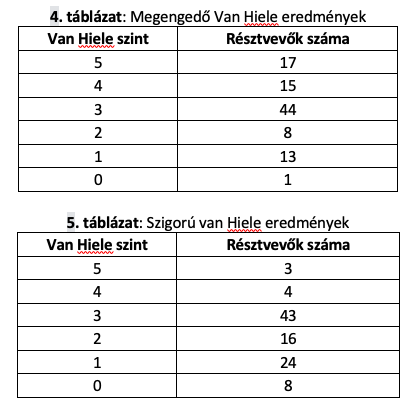
Az eredményekből az látszik, hogy a megengedő és szigorú kiértékeléssel is sok kitöltő a nem besorolható („not fit”) kategóriába került. Sok tanulmányban az ilyen eredményt elérő személyeket is beosztják valamelyik szintre. Ezt úgy teszik, hogy veszik a kitöltő által sikeresen teljesített van Hiele szintek azon legbővebb halmazát, ami alapján már besorolható. Például az 1, 2, 4 szinteket sikeresen teljesítő, alapesetben nem besorolható személy van Hiele szintje az előbb leírtak alapján 2, mivel a 4-es szintet elhagyva az 1, 2 szintek teljesítését kapjuk, ami már az eredeti definíció alapján 2-es van Hiele szintnek felel meg. Vannak olyan tanulmányok, amik ilyen esetben azt mondják, a kitöltő legalább 2. szinten van. Ezt a fajta csoportosítást mi is elvégeztük, így eredményeinket módunk lesz összehasonlítani ezen kutatások eredményeivel is. Ennek a beosztásnak az eredménye megengedő értékeléssel a 4. táblázatban, szigorú értékeléssel az 5. táblázatban látható.

A két különböző számítással kapott – minden kitöltőt besoroló – eredmények átlaga és szórása a 6. táblázatban található.

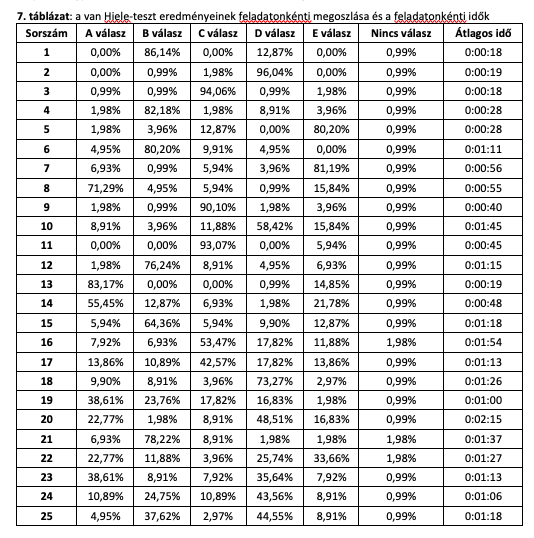
A van Hiele-teszt eredményei mellett az EduBase rendszerének köszönhetően a kitöltés idejét is mérni tudjuk. Az egyes feladatokra adott válaszok százalékos megoszlását a 7. táblázat tartalmazza.

Diszkusszió

Magyarországon Szabó Csaba és munkatársai foglalkoztak legszélesebb körben a geometria megértés szintjeinek vizsgálatával a közoktatásban tanulók esetén ([9]). Megyeri Krisztina a Dr. Ámbédkar Iskola diákjainak gondolkodási szintjét elemezte. Herendiné Kónya Eszter a tanítójelöltek geometria gondolkodási szintjeit elemezte a van Hiele-teszt segítségével ([10]). Szabó és munkatársai egy még nem publikált kutatás keretei között az Eötvös Loránd Tudományegyetem matematika szakos hallgatóit is tesztelték, míg mi a gazdasági képzésben tanuló hallgatók geometriai gondolkodási szintjét igyekeztünk feltérképezni. Minden hazai vizsgálat megállapítja, hogy a diákok geometriai megértési szintje nem a NAT elvárásainak megfelelően alakul.

A gazdasági képzési területen Magyarországon még nem végeztek méréseket és a nemzetközi szakirodalomban sem találtunk ilyen kutatást, így munkánk hiánypótló. A kapott eredmények jobbak a többi hazai mérésnél, viszont még a megengedő kiértékelési módszerrel sem éri el a hallgatók átlaga a negyedik szintet, annak ellenére, hogy a középiskolai tananyag erre a szintre készít/készítene fel, illetve, hogy az erre a szakra felvett hallgatók a felvételi pontok alapján a jobb képességűek közé sorolhatók. Bár sokan vannak köztük, akik elfogadható (négyes, ötös) szinten teljesítettek, a magas szórás azonban azt is jelenti, hogy sok gyenge eredmény is született. Az ilyen hallgatók számára gondot jelent a kalkulus tárgy teljesítése, legfeljebb csak megtanulják, de nem értik a matematikát használó tárgyak összefüggéseit, magasabb lemorzsolódás várható a teszten náluk jobban teljesítő társaikhoz képest.

A vizsgált hallgatók feltételezhetően az átlagnál jobbak, ezért az összes magyarországi hallgatóra vett átlag valószínűleg még alacsonyabb lenne. Ezen hipotézisünk alátámasztására érdemes eredményeinket a Students’ non-development in high school geometry [9] kutatás 12. osztályos tanulókra vonatkozó eredményeivel összevetni. Szabó és munkatársai öt különböző magyarországi közoktatási intézményben (amelyek között művészeti gimnázium is volt) nézték a geometriai megértés szintjeit, minden iskolában több évfolyamon. A tesztek eredményét a miénkkel azonos módon értékelték ki (a nálunk megengedő náluk „weak”, a nálunk szigorú náluk „strong” elnevezést kapta). A nem besorolható kategóriát a szerzők nem alakítottak ki, mindenkit besoroltak valamelyik szintre, ugyanúgy, ahogy mi is megtettük a kompatibilitás érdekében (4., 5., 6. táblázat).

12. évfolyamon az általuk kapott eredmények a megengedő értékeléssel a 8. táblázatban, a szigorú értékeléssel a 9. táblázatban láthatók. Az A, B, C, D, E betűk az öt középiskolát jelölik, azok megnevezése nélkül.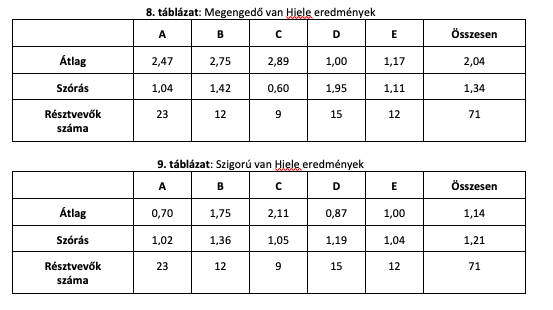       

Konklúzió

Nagyobb hangsúlyt kell fektetni a középiskolai tanulók geometriai gondolkodásának fejlesztésére, mert sokan elmaradnak a NAT-ban kitűzött céloktól, aminek következményeként érettségit követően sem érik el a felsőoktatásban megkívánt szintet. Főleg a matematikával kiemelten foglalkozó szakokat (matematikus, mérnök, gazdasági) választó diákok számára fontos a kompetenciafejlesztés.

Felhasznált szakirodalom

[1]: I. Braun, J. E. Schröder (2014): Cooperation schule hochschule, Baden-Württembergs: Hochschulen Baden-Württembergs,

[2]: Bruner, Jerome Seymour (1966): Toward a Theory of Instruction, Mass.: Belkapp Press. Cambridge

[3]: Bruner, Jerome Seymour (1986): Actual Minds, Possible Worlds, MA: Harvard University Press. Cambridge,

[4]: Bruner, Jerome Seymour (1990): Acts of Meaning. MA: Harvard University Press. Cambridge

[5]: Mayberry, J. (1983): The van Hiele levels of geometric thought in undergraduate preservice teachers, Journal for Research in Mathematics Education, 14, 58–69.

[6]: Fuys, D., Gedde, D. and Tischler, R. (1988): The van Hiele model of thinking in geometry among adolescents, Journal for Research in Mathematics Education Monograph No. 3.

[7]: Burger, W. F. and Shaughnessy, J. M. (1986): Characterizing the van Hiele levels of development in geometry, Journal for Research in Mathematics Education, 17, 31–48.

[8]: Usiskin, Z. (1982): Van Hiele levels and achievement in secondary school geometry, Final Report of the Cognitive Development and Achievement in Secondary School Geometry Project Department of Education, University of Chicago, US.

[9]: Szabó, Cs., Bereczky-Zámbó, Cs., Muzsnay, A. Szeibert, J. (2020), Students’ non-development in high school geometry, Annales Mathematicae et Informaticae, pp. 309-319.

[10]: Kónya, E. (2003), A tanítójelöltek geometriai gondolkodásának jellegzetességei, Iskolakultúra, pp. 51-61.