Anna Lehofer

Decrypting Historical Ciphers - A Way of Mathematical Competence Development

Improving Mathematical Competences

The need and importance of developing key competences already entered public thinking in the early 1990s. On the World Conference on Education, in 1990, the following thought was communicated as a basic learning need: "Every person  –  child,  youth and adult  –  shall be able to benefit from educational  opportunities  designed to meet their basic learning needs. These needs comprise both essential learning tools (such as literacy, oral expression, numeracy, and problem-solving) and the basic learning content (such as knowledge, skills, values, and attitudes) required by human beings to be able to survive, to develop their full capacities, to live and work in dignity, to participate fully in the development, to improve the quality of their lives, to make informed decisions, and to continue learning (World Declaration on Education for All, 1990, p. 3)." Although it was not yet the explicit wording of the need for competence development, the direction was marked out already in 1990.

If we try to find a definition of key competences, we will find many. Many professionals, from many points of view, interpret the notion in different ways. A study about key competences says: "there is no universal definition of the notion of ‘key competence.’ Despite the differing conceptualization and interpretation of the term, the majority of experts seem to agree that for competence to deserve attributes such as ‘key,’ ‘core,’ ‘essential’ or ‘basic,’ it must be necessary and beneficial to any individual and society as a whole. It must enable an individual to successfully integrate into several social networks while remaining independent and personally effective in familiar as well as new and unpredictable settings. And, since all settings are subject to change, a key competence must enable people to constantly update their knowledge and skills to keep abreast of fresh developments (Key competences, 2002, p. 14)."

According to the OECD PISA framework, the basic eight mathematical competences are mathematical  thinking skill, mathematical argumentation skill; modeling skill; problem posing and solving skill; representation  skill; symbolic, formal and technical skill, communication skill, aids, and tools skill. This is a non-hierarchical list of general mathematical skills that are relevant and appropriate to all levels of education. This list includes the following elements and short descriptions (OECD, 1999, p. 43):

·     Mathematical thinking skill. This includes posing questions characteristic of mathematics (“Is there...?”, “If so, how many?”, “How do we find...?”); knowing the kinds of answers that mathematics offers to such questions; distinguishing between different kinds of statements (definitions, theorems, conjectures, hypotheses, examples, conditioned assertions); and understanding and handling the extent and limits of given mathematical concepts.

·     Mathematical argumentation skill. This includes knowing what mathematical proofs are and how they differ from other kinds of mathematical reasoning, following and assessing chains of mathematical arguments of different types, possessing a feel for heuristics (“What can(not) happen, and why?”), and creating mathematical arguments.

·     Modelling skill. This includes structuring the field or situation to be modeled; “mathematizing” (translating “reality” into mathematical structures); “de-mathematizing” (interpreting mathematical models in terms of “reality”); working with a mathematical model; validating the model; reflecting, analyzing and offering a critique of a model and its results; communicating about the model and its results (including the limitations of such results); and monitoring and controlling the modeling process.

·     Problem posing and solving skills. This includes posing, formulating, and defining different kinds of mathematical problems (“pure,” “applied,” “open-ended,” and “closed”); and solving different kinds of mathematical problems in a variety of ways.

·     Representation skill. This includes decoding, interpreting, and distinguishing between different forms of representation of mathematical objects and situations and the interrelationships between the various representations; choosing, and switching between different forms of representation, according to situation and purpose.

·     Symbolic, formal and technical skill. This includes: decoding and interpreting symbolic and formal language and understanding its relationship to natural language, translating from natural language to symbolic/formal language, handling statements and expressions containing symbols and formulae, using variables, solving equations, and undertaking calculations.

·     Communication skill. This includes expressing oneself, in a variety of ways, on matters with mathematical content, in oral as well as in written form, and understanding others’ written or oral statements about such matters.

·     Aids and tools skill. This includes knowing about and being able to make use of, various aids and tools (including information technology tools) that may assist mathematical activity, and knowing about the limitations of such aids and tools.

Among these mathematical competences, especially mathematical thinking skills, problem posing and solving skill, representation skill, symbolic, formal, and technical skills can be improved by classical ciphers in a very effective and spectacular way. In the following, we will corroborate this statement by demonstrating different encryption types on real historical ciphers.

Beyond the relationship between mathematical competences and historical cryptology, due to the interdisciplinary feature of cryptology, classical ciphers are appropriate to improve linguistic, historical, and IT skills as well.

Improving Mathematical Competences with Classical Ciphers

According to the definitions of Craig P. Bauer, cryptography is the science of creating cipher systems. Cryptanalysis is the science and art of breaking ciphers (deciphering without the key). Cryptology embraces both cryptography and cryptanalysis (Bauer, 2013, xix).

Somehow we have to draw a line between classical and modern cryptology. This line is usually drawn somewhere around World War II. Classical cryptography includes the systems and methods introduced before World War II. Many of these systems are still in use (mostly by amateurs), but for the most part, they have been replaced by methods that make use of computers (Bauer, 2013, xxi): this phase is called modern cryptology. According to the less formal definition, classical (or historical) cryptography contains encryption methods that can be decrypted with pencil and paper, i.e., codebreakers do not need a computer to solve them. In contrast, the puzzles of modern cryptology can typically be created and solved by a computer-aided process.

We know about attempts to introduce cryptology into public education. Still, these are typically higher educational instances, and most of these higher educational cases deal with modern cryptology, not the historical part of cryptography and cryptanalysis.

These historical ciphers are sometimes so easy to solve, that even primary school students can understand the encryption and decryption methodologies. However, sometimes even these easy types of historical ciphers remain unsolved, and besides the simpler types of ciphers, there are cipher types that are very challenging to crack. For instance, historians, linguistics, mathematicians, and IT professionals preoccupy with the encryption method of homophonic substitution ciphers even today. Thus a very wide age group (from elementary school to adults/professionals) can be affected and interested in this way of mathematical competence development.

In the following, three different cipher types of the early modern age will be presented with the short demonstration of decryption methods as well. We are moving from simpler cases to more complex ones, which simultaneously points from a simpler mathematical toolbar to a more complex one. With this series of historical examples, we would like to corroborate the statement that historical ciphers are pronouncedly suitable for introducing various mathematical methodologies and can entertain younger and elder audiences evenly.

Simple Substitution Cipher

A simple substitution cipher takes a letter of an alphabet and substitutes it with another letter (or number or any kind of symbol). The ciphertext is generated by this simple substitution process. A plaintext character will be replaced by the same ciphertext character during the entire ciphertext. Since only one code alphabet is used to encrypt the plaintext message, it is usually called a monoalphabetic cipher.

Let us see a historical example from the early modern age. This letter was written around 1664-1668 in connection with the Wesselényi conspiracy in an encrypted way[1].

Figure 1 - Excerpt from the simple substitution cipher

If we want to decrypt this message, the first thing we have to do is to count the different code characters. After this counting process, we will know how many different code characters does the message use and how long the encrypted text is. This 750 character-long simple substitution cipher uses 25 different code characters and contains the exclusively enciphered text. Since simple substitution is an easy way of encryption, we can even take a pencil and a piece of paper to count these parameters by hand/manually. We are curious about the frequencies of the individual code characters and the bigrams, trigrams, n-grams that appear in the text several times/repeatedly. Sometimes these recurring character lines can be the breaking point into the encrypted text.

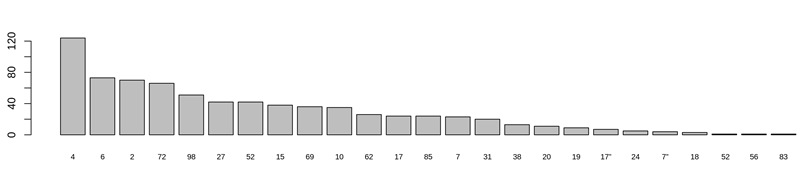Figure 2 - Frequency analysis of the code characters

Since this manuscript is presumably written in Hungarian, we will check the letter frequencies of the Hungarian language and compare it to the code character frequencies. In the Hungarian language, the most common letters are (in order): e, a, t, n, l, o. In the ciphertext, the most common code character is '4'. This character represents the letter 'e' in the plaintext with a very high probability. The second most frequent code character in the text is '6'. It probably stands for 'a' in the plaintext, and so on. In this cipher, '4' represents 'e' indeed, and '6' represents 'a.' The code character '2' stands for 'i', '72' for 'n', '98' form'. Based on these probabilities, we are already able to seek meaningful phrases, word parts. But if it proves insufficient - often because of the shortness of the ciphertext - we can analyze the n-grams in the ciphertext. This means that we prepare frequency analysis for bigrams, trigrams, and so on. This way, we will also find the longest character lines that appear several times in the ciphertext and can be with a high probability a breaking point into the ciphertext.

In the case of this monoalphabetic substitution letter, the n-gram statistics show that the character line [27 4 62 2 4 52 98 4 31] appears three-times in the text. If our letter frequency analysis is correct, the code character '4' presumably stands for 'e', '2' for 'i', '98' form'. If we substitute these letters into the character line, we will get: [27 e 62 I e 52 m e 31]. If someone is familiar with the early modern Hungarian written language and with certain courtesy habits of the ancestors, they can easily find the missing parts of this word. The word is 'kegielmed', which nowadays would be written as 'kegyelmed'. This word means 'your grace' which was a courteous accost that time.

From this point success is at our fingertips. We know the plaintext equivalents of seven code characters, so based on the outlined wordpatterns and word fragments, we just have to find the plaintext equivalents of the code characters that form a meaningful text.

If, for some reason the aforementioned techniques do not bring the break-through, a vowel identification can also be performed. A very detailed description of this technique can be found in an American field manual (Basic Cryptanalysis, 1990, pp. 4-32).

Polyalphabetic Substitution Cipher

A polyalphabetic cipher is also based on substitution but uses multiple code alphabets (cipher alphabets). When encrypting a plaintext message, at each plaintext letter, we change the code alphabet according to some system.  All the alphabets were usually written out in a large 26x26 table (since for the 26 letters, 26 different cipher alphabets were accessible).

Probably the most popular polyalphabetic substitution cipher is the one Blaise de Vigenère created in the 16th century. For a long time, it was called "le Chiffre indéchiffrable" since it was thought to be indecipherable. What we call Vigenère cipher nowadays is something easier than the original system of Vigenère.

In the wording of Kahn: the Vigenère cipher employs only standard alphabets and a short repeating keyword. Its table consists of 26 standard horizontal alphabets; each slid one space to the left of the one above. These are the cipher alphabets. A normal alphabet for the plaintext stands at the top. Another normal alphabet, which merely repeats the initial letters of the horizontal ciphertext alphabets, runs down the left side. This is the key alphabet. Both correspondents must know the keyword. The encipherer repeats this above the plaintext letters until each one has a key letter. He seeks the plaintext letter in the top alphabet and the key letter in the side. Then he traces down from the top and in from the side. The ciphertext letter stands at the intersection of the column and the row. The encipherer repeats this process with all the letters of the plaintext. To decipher, the clerk begins with the key letter, runs in along the ciphertext alphabet until he strikes the cipher letter, then follows the column of letters upward until he emerges at the plaintext letter at the top (Kahn, 1967, p. 148).

Figure 3 - The Kryptos sculpture

The first message (marked with green) and the second message (marked with yellow) can be found on the left block of the whole kryptos text. On the right side of the copper plate, the Vigenère table can be found. This table contains the shifted alphabets of this polyalphabetic cipher. The alphabets are not just shifted letter by letter but are arranged for the word "kryptos". Now the sequence of the alphabets is known, but the keyword is still missing, which is the hardest phase in the decryption of a Vigenère cipher.

Figure 4 - The two Vigenère ciphers in the whole Kryptos transcription[2]

The Vigenère cipher - as a type of encryption - remained unsolved for a long time. Charles Babbage - a mathematician, philosopher, inventor, and mechanical engineer - was the person who finally found the decryption method of "le chiffre indéchiffrable" around 1854. The basic idea of Babbage was that if our ciphertext was long enough, and the length of the keyword was somewhere between 2 and 26, we could probably find recurring sequences in the ciphertext. These recurrences were the clue for Babbage that led to the decipherment of the Vigenère cipher.

The first step is to look for recurring character lines. If we find some, we can suppose that these character lines recur because they were encrypted with the same code alphabet. We can prepare a table where these recurring sequences are listed with the spacing between the recurrences. We also have to look at the factors of all the spacings. The number which is indicated in all cases will be the most probable keyword length.

Now we probably know the length of the keyword but still do not know the word. So as a second step, we take our Vigenère cipher apart. Since each letter of the keyword is providing a different cipher alphabet for encryption, we can say we have as many monoalphabetic substitution ciphers in a Vigenère cipher as many characters the keyword consists of.

Thus the Vigenère cipher can be handled as a bunch of monoalphabetic substitution ciphers, which we already know how to cryptanalysis. Using a simple frequency analysis on each "monoalphabetic part" of the whole Vigenere cipher, we can compare the code character frequencies with the English letter frequencies. Based on these frequency values, we just have to find how many characters the cipher alphabet is shifted compared to the original alphabet. With the help of the diagrams' shape - peaks, valleys, plateaus - we can find where the two diagrams correspond to each other the best. If our comparison is correct, we can find the plaintext equivalents of the code characters, thus the letters of the keyword, if we repeat this process as many times as the length of the keyword requires.

As we finished the lingering letter identification process of the keyword, we simply have to do the substitution as the third and final step.[3]

The keywords for the first two encrypted messages of Kryptos are PALIMPSEST for the first part, ABSCISSA, for the second part. If we know these parameters, we just have to sort the alphabets by the keywords' letters and do the substitution. Thus the solution of the first cipher sounds like this: "Between subtle shading and the absence of light lies the nuance of illusion." and the second ciphers is: "It was invisible. How’s that possible? They used the earth’s magnetic field. x The information was gathered and transmitted underground to an unknown location. x Does Langley know about this? They should: it’s buried out there somewhere. x Who knows the exact location? Only WW. This was his last message. x Thirty eight degrees fifty-seven minutes six point five seconds north, seventy-seven degrees eight minutes forty-four seconds west. x Layer two."[4]

Homophonic Substitution Cipher

In a homophonic substitution cipher single plaintext letters map to more than one code character (ciphertext symbol). In simpler cases, only the vowels and the most frequent letters were replaced with more than one code character. Still, in an advanced, complex cipher key, each of the plaintext letters maps to several code characters, so-called homophones in the ciphertext. In this case, the frequency distribution is flattened, making the task of the codebreakers much harder (s more difficult). Our example is a homophonic substitution cipher from 1664-1668. This letter's cipher key used homophones only for the vowels and used all in all 40 different code characters for 20 different plaintext letters. The frequency analysis of the code characters shows interesting results.

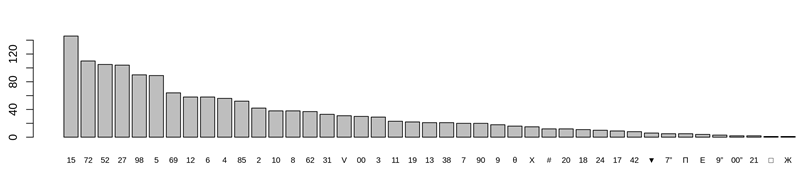Figure 5 - Distribution of the code characters in the homophonic substitution cipher

We were expecting a flattened distribution, but the results show a similar distribution that we experienced at the simple substitution cipher. A possible reason for this is the brevity of the text and the inaccurate use of the cipher key. In many cases, we face the phenomenon that the persons who encrypted these letters hundreds of years ago, used the cipher key in an improper or comfortable way: the key offered much stronger encryption than the encoder took advantage of. In this case, only the five vowels were replaced with several homophones (five homophones each). Still, these homophones were not used in an equal proportion during the encryption: some of them were prioritized, others were nearly ignored. That is why the shape of the diagram is very similar to the simple substitution distribution, but these code character frequencies do not follow the plaintext letter frequencies. The most frequent code characters stand for 't', 'n', 'l', 'k' and 'm'. The first vowel only appears in the 6th column. So instead of the uneven frequencies Figure 5 shows, these statistics will not help when we try to compare them with the plaintext letter frequencies.

Because of these circumstances, the methods that can help to decrypt a monoalphabetic substitution cipher are often too weak to find a breaking point into a homophonic substitution cipher. An additional decryption tool has to be involved. Among other possibilities, hierarchical clustering can bring some results in this case. The first time when hierarchical clustering was successfully used to decrypt a homophonic substitution cipher was the decryption of the famous Copiale code[5].

Let us see how hierarchical clustering can support the decryption process. As Kumar formulates, cluster analysis groups data objects based only on information found in the data that describes the objects and their relationships. The goal is that the objects within a group be similar (or related) to one another and different from (or unrelated to) the objects in other groups. The greater the similarity (or homogeneity) within a group and the greater the difference between groups, the better or more distinct the clustering (Kumar et al., 2005, p. 490). Speaking of homophonic substitution ciphers, the context of the particular code characters was investigated.

To display hierarchical clustering graphically, the open-source Cran R[6] software was used, which visualizes the relationships as dendrograms. Each element on the bottom of the dendrogram represents a coded character. Looking at the dendrograms, we can separate different clusters. Each cluster consists of similar code characters. This similarity is based on the code characters' contexts: left and right neighborhoods. Height represents the level of the hierarchy, normalized from 0 to 1.

The vowel-consonant difference shows up high in the cluster map, smaller clusters low in the cluster map indicate very high similarity (e.g., homophone groups standing for one plaintext letter).

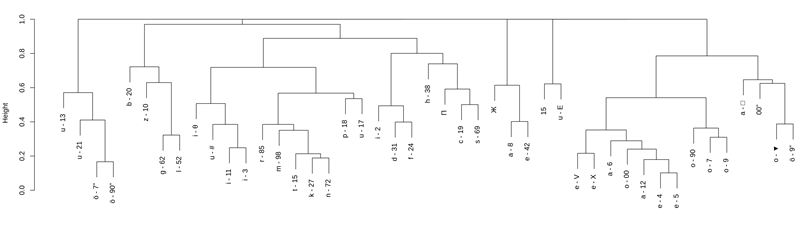Figure 6 - Dendrogram of the homophonic substitution cipher

In our case, the clustering process splits the code characters into two bigger and three smaller clusters. The three smaller clusters group the code characters that were difficult to classify. That is why these small clusters are not in the focus of our interest. However, the two big clusters represent the essence of this examination. The big cluster on the right contains exclusively vowels, the other big cluster on the left contains almost exclusively consonants (1 mistake[7] out of 22 elements which mean an efficiency over 95%). In some cases, even the homophone groups belonging to the particular plaintext letters are also identified correctly (see the smaller sub-clusters within the big clusters, e.g., the [7, 9, 90] homophone group that represents the letter 'o' in the plaintext).

Conclusion

After we learned the essence of simple, polyalphabetic, and homophonic substitution ciphers and also met the methods these ciphers can be cryptanalysis with, we can state that the discipline of cryptology is full of encryption and decryption methods that can demonstrate various mathematical issues. Since cryptology is a mysterious and interesting discipline by its nature, it can effectively and efficiently be used to be a basis for mathematical competence development. Since history has been handed down to us plenty of various encrypted manuscripts, we can even decide for which age group, or how difficult competence development we aim at.

Acknowledgements

This work has been supported by the Swedish Research Council, grant 2018-06074, DECRYPT - Decryption of historical manuscripts.

References

·        Basic Cryptanalysis (Field Manual No. 34-40-2). Washington, DC: Headquartes Department of the Army, 1990.

·        Bauer, Craig P. Secret History: The Story of Cryptology. Boca Raton, FL: CRC Press, 2013.

·        Kahn, David. The Codebreakers. The story of Secret Writing. New York: Scribner, 1996.

·        Key Competences. A developing concept in general compulsory education. Brussels, Belgium: Eurydice European Unit, 2002.

·        Kumar, Vipin, Michael Steinbach, Pang-Ning Tan. Introduction to Data Mining. Boston: Pearson (Education Inc.), 2005.

·        Láng, Benedek. Titkosírás a Kora Újkori Magyarországon. Budapest: Balassi Kiadó, 2015.

·        OECD: Measuring Student Knowledge and Skills – A new Framework for Assessment. Paris, France: OECD, Programme for International Student Assessment (PISA), 1999.

·        Singh, Simon. The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography. New York: Anchor Books, 2000.

·       World Declaration on Education for All. Framework for Action to Meet Basic Learning Needs. New York: UNESCO, 1990.

Appendix

Transcription of the simple substitution cipher

85 . 6 . 27 . 7 . 19 . 10 . 2 . 17 . 6 . 52 . 4 . 72 . 69 . 10 . 4 . 98 . 20 . 4 . 72 . 17 . 7 . 52 . 15 . 6 . 98 . 31 . 4 . 6 . 10 . 98 . 2 . 72 . 31 . 4 . 72 . 4 . 27 . 4 . 15 . 52 . 4 . 15 . 7” . 15 . 27 . 4 . 10 . 4 . 85 . 17” . 52 . 4 . 69 . 98 . 6 . 62 . 6 . 72 . 7 . 69 . 69 . 6 . 72 . 6 . 27 . 6 . 85 . 52 . 4 . 72 . 72 . 2 . 6 . 10 . 98 . 2 . 72 . 15 . 38 . 7 . 62 . 2 . 6 . 10 . 4 . 52 . 98 . 17 . 52 . 15 . 18 . 4 . 72 . 15 . 4 . 27 . 4 . 72 . 6 . 10 . 6 . 72 . 72 . 2 . 6 . 17 . 6 . 52 . 4 . 62 . 2 . 17” . 15 . 15 . 7 . 27 . 6 . 2 . 20 . 72 . 6 . 10 . 72 . 4 . 98 . 4 . 15 . 4 . 27 . 72 . 4 . 27 . 83 . 7 . 18 . 4 . 72 . 10 . 15 . 17 . 2 . 15 . 6 . 10 . 19 . 10 . 6 . 69 . 10 . 6 . 85 . 85 . 4 . 56 . 17 . 2 . 69 . 2 . 15 . 2 . 7 . 2 . 6 . 85 . 6 . 4 . 69 . 6 . 10 . 69 . 10 . 6 . 27 . 98 . 6 . 85 . 2 . 6 . 27 . 72 . 6 . 27 . 2 . 69 . 24 . 2 . 10 . 4 . 15 . 72 . 2 . 24 . 7 . 62 . 6 . 10 . 6 . 72 . 72 . 2 . 6 . 6 . 10 . 15 . 7” . 85 . 7” . 27 . 98 . 4 . 62 . 98 . 7 . 69 . 15 . 2 . 69 . 20 . 2 . 10 . 15 . 6 . 15 . 4 . 69 . 6 . 69 . 69 . 4 . 19 . 17 . 85 .  52 . 31 . 4 . 6 . 10 . 27 . 4 . 62 . 2 . 4 . 98 . 4 . 31 . 2 . 72 . 19 . 52 . 17 . 69 . 6 . 2 . 20 . 17 . 52 . 98 . 6 . 69 . 15 . 52 . 6 . 15 . 7 . 27 . 4 . 85 . 31 . 4 . 52 . 2 . 20 . 4 . 72 . 2 . 69 . 98 . 2 . 72 . 31. 2 . 85 . 15 . 17 . 72 . 27 . 98 . 2 . 72 . 31 . 2 . 10 . 4 . 72 . 15 . 17” . 72 . 27 . 31 . 4 . 6 . 10 . 2 . 69 . 19 . 10 . 6 . 27 . 85. 4 . 98 . 4 . 72 . 69 . 4 . 62 . 38 . 6 . 72 . 4 . 98 . 19 . 10 . 6 . 27 . 98 . 6 . 69 . 98 . 4 . 31 . 2 . 17 . 98 . 98 . 6 . 52 . 27 . 4 . 52 . 4 . 52 . 4 . 2 . 15 . 17 . 4 . 72 . 72 . 2 . 17 . 4 . 69 . 10 . 4 . 31 . 4 . 52 . 98 . 17” . 72 . 27 . 72 . 4 . 27 . 98 . 4 . 72 . 72 . 4 . 52 . 38. 6 . 98 . 6 . 85 . 6 . 20 . 2 . 69 . 15 . 4 . 72 . 4 . 85 . 15 . 52 . 4 . 62 . 2 . 4 . 72 . 62 . 7 . 72 . 62 . 2 . 6 . 85 . 4 . 6 . 98 . 27 . 4 . 62 . 2 . 4 . 52 . 98 . 4 . 31 . 72 . 4 . 27 . 98 . 4 . 85 . 15 . 72 . 4 . 27 . 4 . 98 . 2 . 15 . 4 . 52 . 27 . 4 . 52 . 17 . 4 . 69 . 10 . 72 . 4 . 98 . 4 . 69 . 2 . 85 . 2 . 7 . 72 . 6 . 10 . 98 . 2 . 27 . 4 . 62 . 2 . 4 . 52 . 98 . 4 . 69 . 6 . 69 . 69 . 10 . 7 . 72 . 2 . 17 . 72 . 27 . 72 . 6 . 27 . 2 . 69 . 4 . 52 . 4 . 15 . 4 . 98 . 24 . 4 . 52 . 7” . 52 . 20 . 2 . 10 . 7 . 72 . 2 . 98 . 4 . 62 . 38 . 6 . 52 . 6 . 52 . 7 . 98 . 38 . 6 . 17 . 6 . 52 . 6 . 98 . 2 . 62 . 4 . 52 . 38 . 4 . 15 . 4 . 27 . 4 . 17 . 4 . 52 . 18 . 4 . 72 . 2 . 62 . 38 . 6 . 27 . 4 . 69 . 17” . 72 . 27 . 4 . 52 . 17 . 4 . 69 . 10 . 17” . 72 . 27 . 72 . 4 . 27 . 4 . 98 . 4 . 62 . 2 . 4 . 31 . 17” . 52 . 19 . 10 . 6 . 27 . 27 . 4 . 62 . 2 . 4 . 52 . 98 . 4 . 31 . 20 . 4 . 72 . 98 . 2 . 72 . 31 . 4 . 72 . 85 . 4 . 98 . 4 . 72 . 69 . 4 . 62 . 4 . 98 . 38 . 6 . 17 . 62 . 2 . 6 . 72 . 72 . 4 . 38 . 4 . 10 . 4 . 31 . 2 . 27 . 6 . 10 . 31 . 7 . 52 . 7 . 62 . 4 . 72 . 2 . 69 . 38 . 6 . 31 . 24 . 4 . 85 . 2 . 4 . 27 . 20 . 4 . 4 . 62 . 2 . 27 . 2 . 69 . 27 . 7 . 85 . 2 . 69 . 98 . 17 . 85 . 6 . 72 . 2 . 20 . 6 . 72 . 52 . 4 . 52 . 27 . 4 . 98 . 24 . 2 . 6 . 98 . 17 . 85 . 6 . 98 . 2 . 85 . 2 . 7 . 72 . 4 . 69 . 15 . 17 . 31 . 7 . 69 . 2 . 19 . 10 . 7 . 72 . 27 . 4 . 62 . 2 . 52 . 98 . 4 . 31 .15 . 17 . 62 . 2. 6 . 98 . 98 . 2 . 72 . 15 . 20 . 2 . 10 . 38 . 6 . 15 . 7 . 98 . 72 . 4 . 38 . 6 . 62 . 2 . 7 . 72 . 4 . 52 . 27 . 4 . 62 . 2 . 4 . 52 . 98 . 4 . 31 . 15 . 6 . 85 . 19 . 10 . 6 . 98 . 4 . 62 . 4 . 52 . 4 . 15 . 4 . 98 . 4 . 15 . 17 . 6 . 52 . 6 . 98 . 2 . 72 . 15 . 52 . 4 . 38 . 4 . 15

Key of the simple substitution cipher

2 – I

4 – E

6 – A

7 – O

7” – Ö

10 – Z

15 – T

17 – U

17” – Ü

18 – P

19 – C

20 – B

24 – F

27 – K

31 – D

38 – H

52 – L

56 – Q

62 – G

69 – S

72 – N

83 – J

85 – R

98 –

Transcription of the homophonic substitution cipher

20 . V . 72 . 52 . 5 . 17 . 4 . 72 . 72 . X . 98 . 98 . 00 . 72 . 31 . 9 . 15 . 15 . 6 . 98 . 27 . 62 . 27 . 12 . 10 . ▼ . 15 . 13 . 12 . 52 . 7 . 69 . 90 . 27 . 31 . 11 . 69 . 15 . 85 . 6 . 19 . 15 . θ . 7 . 72 . 6 . 27 . 15 . 21 . 52 . П . 3 . 31 . 9 . 72 . 2 . 15 . 00 . 98 . 98 . 3 . 31 . ▼ . 72 . 69 . 13 . 20 . 69 . 19 . 85 . 18 . 15 . 3 . 7 . 2 . 12 . 6 . 52 . 12 . 15 . # . 12 . 52 . 90 . 19 . 9 . 19 . 69 . 27 . 90 . 69 . 52 . 5 . 17 . 4 . 52 . 5 . 15 . 98 . 8 . 52 . 19 . 9 . 72 . 24 . 4 . 85 . 8 . 52 . 72 . 12 . 98 . 6 . 72 . 72 . 12 . 27 . □ . 52 . 27 . 8 . 52 . 98 . 8 . 15 . 00 . 69 . 69 . 6 . 62 . 6 . 13 . 6 . 52 . 2 . V . 52 . X . 72 . 15 . 5 . 15 . 15 . 4 . 00 . 27 . X . 62 . 52 . 98 . X . 98 . 2 .  72 . V . 98 . 00 . 69 . 9 . 27 . 15 . 90 . 27 . 5 . 52 . 52 . 4 . 15 . 52 . 4 . 72 . 38 . 3 . 85 . 4 . 27 . V . 15 . 38 . 2 . 72 . 15 . 5 . 62 . 4 . 15 . 15 . 5 . 27 . X . 72 . 24 . 4 . 52 . 90 . 52 . 5 . 98 . 69 . ▼ . 15 . 69 . 10 . 12 . 52 . 12 . 69 . 12 . 85 . 9 . 52 . 19 . 7 . 72 . 24 . 3 . 31 . 4 . 72 . 15 . ▼ . 85 . θ . 85 . 13 . 12 . 72 . 00 . 27 . X . 62 . 98 . 42 . 72 . 5 . 98 . 4 . 52 . 52 . 2 . 5 . 27 . 4 . 15 . θ . 85 . 6 . 69 . 20 . 6 . 72 . 2 . 69 . 98 . V . 62 . 2 . 4 . 52 . 5 . 72 . 15 . 5 . 15 . 15 . 38 . 8 . 69 . ▼ . 98 . 52 . 90 . 27 . 12 . 15 . 85 . 5 . 24 . 4 . 85 . 6 . 52 . 15 . 98 . 8 . 62 . 12 . 2 . 69 . 27 . 62 . 52 . 31 . 98 . 3 . 27 . 5 . 15 . 2 . 85 . 90 . 19 . 69 . 27 . 12 . 52 . 15 . 12 . 27 . 72 . 5 . 98 . 4 . 52 . 52 .  2 . 4 . 27 . 5 . 72 . 4 . 52 . 52 . V . 5 . 98 . 98 . 5 . 52 . 15 . 9 . 69 . 6 . 62 . 90 . 69 . 72 . 12 . 27 . 6 . 10 . 38 . 8 . 85 . 00 . 98 . 24 . 4 . 52 . 00 . 00 . # . П . 52 . 90 . 31 . 7 . 52 . 90 . 62 . V . 62 . 2 . 7 . 17 . 5 . 19 . 9 . 72 . 19 . 13 . 85 . 85 . 8 . 52 . 17 . 72 . 6 . 10 . V . 85 . 15 . θ . 85 . 15 . 12 . 98 . 4 . 85 . 10 . 5 . 27 . V . 72 . 72 . X . 52 . 72 . 12 . 27 . 98 . V . 85 . 15 . X . 85 . 5 . 15 . 72 . 4 . 27 . 72 . 5 . 27 . 69 . 00 . 15 . 72 . 12 . 27 . 11 . 69 . 6 . 72 . 72 . 3 . 00 . 20 . 52 . 2 . 62 . 6 . 15 . 9 . 85 . 11 . 6 . 2 . 12 . 85 . 8 . 69 . 7” . 15 . 19 . 90 . 85 . 18 . 7 . 85 . 8 . 52 . 5 . θ . # . 85 . 8 . 98 . 5 . 72 . 15 . # . 98 . 8 . 85 . 6 . 98 . 5 . 52 . 52 . 24 . 15 . 98 . 8 . 85 . 15 . 90” . 52 . 5 . 98 . # . 4 . 15 . 15 . 5 . 27 . 38 . 3 . 72 . 72 . 2 . 27 . 9” . 52 . 52 . 4 . 72 . 5 . П . 38 . 9 . 10 . 00 . 52 . 2 . 31 . 4 . 98 . 7 . 72 . 69 . 15 . 85 . 8 . 15 . 3 . 7 . 27 . 12 . 15 . 15 . 5 . 15 . 15 . 5 . 98 . 98 . 11 . 72 . 31 . 42 . 52 . 5 . 15 . 4 . 98 . 5 . 15 . V . 85 . 15 . 5 . 27 . 4 . 98 . 5 . 15 . 27 . 7 . 19 . 10 . 27 . 12 . 85 . 8 . # . 5 . 15 . 4 . 15 . 15 . 5 . 98 . X . 69 . 98 . 5 . 62 . 2 . 69 . 3 . 72 . 27 . 12 . 20 . 13 . 12 . 62 . 2 . 00 . 72 . 38 . 3 . 15 . 5 . 52 . 4 . 6 . 10 . X . 52 . 52 . V . 72 . 4 . 98 . 6 . 85 . 90 . 52 . 27 . 7 . 31 . 90 . 27 . 72 . 12 . 27 . 98 . 3 . 85 . 5 . 72 . 4 . 10 . 17 . 5 . 6 . 10 . 15 . θ . 85 . 15 . 12 . 98 . 72 . 12 . 27 . V . 72 . 27 . 4 . 69 . 10 . # . 6 . 62 . 2 . 00 . 27 . 6 . 10 . 31 . 00 . 52 . 62 . 9 . 27 . 20 . 13 . 52 . 27 . 3 . 6 . 52 . 52 . 12 . 72 . 2 . 6 . 10 . 15 . 3 . 15 . 27 . 7 . 27 . 12 . 15 . 98 . 5 . 52 . 52 . 2 . 5 . 27 . 4 . 15 . V . 31 . 31 . 3 . 62 . 15 . 13 . 15 . 15 . 6 . 98 . 98 . 42 . 62 . 15 . 6 . 85 . 15 . 6 . 72 . 9 . 98 . 72 . 4 . 98 . 98 . 3 . 72 . 15 . П . 10 . θ . 00 . V . 69 . 72 . 12 . 52 . 38 . 3 . 38 . V . 15 . 38 . 5 . 15 . 52 . 72 . 52 . 5 . 62 . 2 . 5 . 27 . V . 10 . 13 . 62 . 3 . 15 . 5 . 19 . 10 . 2 . 27 . 69 . 13 . 20 . 69 . 15 . 6 . 72 . 15 . 3 . 12 . 2 . 6 . 8 . 10 . 98 . 2 . 15 . 72 . 12 . 27 . θ . 85 . 15 . 12 . 98 . 27 . 62 . 52 . 31 . 98 . 8 . 62 . 8 . 20 . 7” . 52 . 19 . 69 . 11 . 15 . 3 . 52 . 5 . 15 . 2 . 85 . 4 . 38 . 8 . 62 . θ . 00 . 98 . V . 31 . X . 69 . 98 . 42 . 69 . 15 . 5 . 85 . 38 . 8 . 72 . 5 . 98 . 27 . 7” . 52 . 52 . 5 . 5 . 4 . 72 . 5 . 27 . 4 . 98 . 5 . 10 . 15 . 85 . 5 . 69 . 4 . 72 . 15 . 11 . 6 . 52 . 72 . 00 . 98 . 27 . 2 . 13 . 8 . 52 . 15 . 27 . 5 . 18 . 18 . 4 . 72 . 69 . 9 . 27 . # . 15 . 6 . 27 . 00 . 72 . 15 . 12 . 18 . 8 . 69 . 10 . 15 . 6 . 52 . 13 . 12 . 72 . 31 . 5 . 85 . 5 . 27 . 27 . 6 . 15 . 15 . 00 . 52 . 5 . 98 . 5 . 52 . 15 . 3 . 15 . 27 . ▼ . 52 . 15 . 12 . 27 . 5 . 69 . 6 . 10 . 7 . 27 . 12 . 15 . 98 . 8 . 69 . 9 . 27 . 15 . 17 . 52 . 4 . 69 . 98 . 8 . 69 . 38 . 00 . 72 . 72 . 6 . 72 . 15 . # . 31 . 15 . 12 . 98 . # . θ . 69 . 10 . 7 . 72 . 15 . 5 . 52 . 4 . 15 . 4 . 98 . E . 5 . 69 . 10 . 4 . 31 . 5 . 52 . 98 . 3 . 13 . V . 52 . 6 . 10 . 98 . 5 . 52 . 2 . 15 . θ . 15 . 27 . 90 . 27 . 12 . 15 . 11 . 4 . 52 . 5 . 72 . 15 . 5 . 15  . 15 . 5 . 98 . 15 . 11 . 15 . 00 . 27 . 72 . 12 . 27 . 72 . 4 . 98 . 15 . 12 . 85 . 15 . 7 . 15 . 15 . 12 . 27 . 6 . 10 . 00 . 85 . 5 . 72 . 31 . 11 . 69 . 10 . 98 . 3 . 72 . 4 . 27 . 9 . 27 . 12 . 5 . 85 . 15 . 27 . 62 . 52 . 31 . 69 . 4 . 98 . 5 . 52 . 18 . 85 . 7 . 69 . 4 . 98 . 18 . V . 85 . E . 5 . 62 . 2 . 5 . 27 . 2 . 21 . 3 . 69 . 10 . 8 . 11 . 6 . 15 . 38 . 8 . 38 . 13 . 15 . 7” . 27 . 72 . 5 . 27 . 5 . 52 . 4 . 62 . 5 . 15 . 6 . 27 . 8 . 85 . 72 . 8 . 27 . 15 . 5 . 72 . 72 . 2 . 6 . 62 . 6 . 52 . 52 . 2 . 12 . 72 . 6 . 27 . 13 . 62 . 2 . 6 . 10 . 98 . 11 . 72 . 15 . 6 . 72 . 27 . 6 . 27 . 85 . 5 . 72 . 31 . 3 . 38 . 90 . 52 . 9 . 15 . 18 . 5 . 31 . 2 . 62 . 52 . 5 . 72 . 72 . 2 . 72 . 19 . 69 . 38 . 3 . 15 . 4 . 52 . 5 . 98 . 72 . 12 . 52 . 00 . 27 . 27 . 2 . 6 . 20 . 20 . 17 . 52 . 52 . 12 . 19 . 10 . 11 . 27 . 15 . 7 . 52 . 9” . 98 . 15 . 11 . 15 . 27 . 7 . 52 . 13 . 12 . 19 . 69 . 4 . 52 . 5 . 27 . 5 . 69 . 10 . 72 . V . 27 . 69 . 9 . 27 . 00” . 31 . 9” . 15 . 7” . 52 . 24 . 90 . 62 . 13 . 12 . 98 . 11 . 72 . 31 . X . 72 . V . 27 . 4 . 15 . 42 . 72 . 38 . 8 . 10 . 8 . 98 . 69 . 10 . 9 . 52 . 62 . 6 . 52 . 6 . 15 . 15 . 8 . 72 . 8 . 27 . 98 . 8 . 69 . E . 15 . 15 . 3 . 12 . 15 . 11 . 69 . 15 . 12 . 52 . 6 . 52 . 00 . 98 . 69 . # . 62 . 2 . 12 . 72 . 6 . 10 . 7 . 27 . 15 . 13 . 52 . 27 . 2 . 27 . 72 . 5 . 27 . V . 98 . 38 . 3 . 69 . 10 . 72 . V . 27 . X . 52 . 72 . 42 . 98 . 69 . 10 . 6 . 27 . 12 . 31 . 00 . 27 . 38 . 8 . 27 . 62 . 31 . 72 . 4 . 27 . 15 . 5 . 19 . 10 . 11 . 27 . θ . 72 . 69 . 18 . 4 . 19 . 3 . V . X . 10 . 42 . 72 . 19 . θ . 24 . 85 . 8 . 27 . 6 . 15 . 27 . 13 . 52 . 31 . 38 . V . 15 . 11 . 72 . 12 . 62 . 2 . 24 . 5 . 85 . 4 . 72 . 19 . 72 . 5 . 27 . 98 . 11 . 31 . 00” . 72 . 20 . 6 . 72 . 72 . 12 . 27 . 4 . 72 . 6 . 10 . 90 . 72 . 19 . V . 31 . 13 . 52 . 12 . 15 . θ . 85 . 15 . 8 . 98 . 8 . 27 . 90 . 85 . 98 . 4 . 62 . 6 . 52 . 2 . 18 . 19 . 69 . V . θ . 31 . 00 . 52 . 90 . 62 . 20 . 6 . 72 . 69 . V . 98 . 98 . 11 . 15 . 69 . 5 . 98 . 15 . # . 31 . 15 . 6 . 98 . П . 10 . V . 85 . 15 . 69 . 42 . 98 . 98 . Ж . 31 . 11 . 69 . 62 . 11 . 69 . 15 . 13 . 69 . 15 . 72 . 5 . 98 . 98 . E . 15 . 12 . 15 . 15 . 12 . 98 . 72 . 5 . 98 . 11 . 69 . 98 . 17 . 15 . 12 . 15 . 00 . 27 . 98 . V . 52 . 52 . 2 . 4 . 15 . 27 . 27 . 18 . 85 . 00 . θ . 72 . 24 . 90 . 85 . 98 . 8 . 15 . 11 . 7 . 72 . X . 15 . 17 . 31 . 72 . 2 . 27 . 00 . 52

Key of the homophonic substitution cipher

A – 6 12 □ 8 Π

B – 20

C – 19

D – 31

E – 4 42 5 X V

F – 24

G – 62

H – 38

I – 2 11 3 θ Ж

K – 27

L – 52

M – 98

N – 72

O – 7 90 9 00 ▼

P – 18

R – 85

S – 69

T – 15

U – 17 13 21 E #

Z –

[1] ÖStA HHStA Ung. Akt. Spec. Verschwörerakten VII. Varia Fasc. 327. Konv. D. Chiffres 1664-1668. fol. 62. (Láng, 2015, p. 279)

[2] You can find the editable Kryptos transcription on Elonka Dunin's homepage: https://elonka.com/kryptos/transcript.html

[3] See the detailed description: Singh, 2000, pp. 83-96.

[4] You can find the solution of the first three messages here for instance: https://en.wikipedia.org/wiki/Kryptos#Solutions

[5] The Copiale Cipher is a 105-pages long manuscript containing all in all around 75000 characters, using 90 different code characters. It was decrypted by Kevin Knight, Beáta Megyesi and Christiane Schaefer, presented on the 4th Workshop on Building and Using Comparable Corpora. Portland, Oregon, 2011.

[6] R can be freely downloaded from the website https://cran.rapporter.net/

[7] In the early modern Hungarian language 'u' usually stands for 'v' and letter 'i' represents 'j'. So the letters 'u' and 'i' are correctly grouped into this consonant cluster.